Density Altitude Calculator

Air Temperature:

Humidity Input Type:

Dew Point:

Altimeter Setting:

Station Elevation:

Air Density (\( \rho \)):

Relative Density:

(dimensionless)

Absolute Pressure (\( P_a \)):

Density Altitude:

1. What is the Density Altitude Calculator?

Definition: This calculator computes the air density (\( \rho \)), relative density, absolute pressure (\( P_a \)), and density altitude based on the air temperature, humidity (either dew point or relative humidity), altimeter setting, and station elevation. Density altitude represents the altitude in the International Standard Atmosphere (ISA) where the air density matches the current conditions, affecting aircraft performance.

Purpose: It is used in aviation to assess how atmospheric conditions impact aircraft performance, such as lift, engine power, and takeoff distance, ensuring safe flight planning.

2. How Does the Calculator Work?

The calculator uses the following formulas:

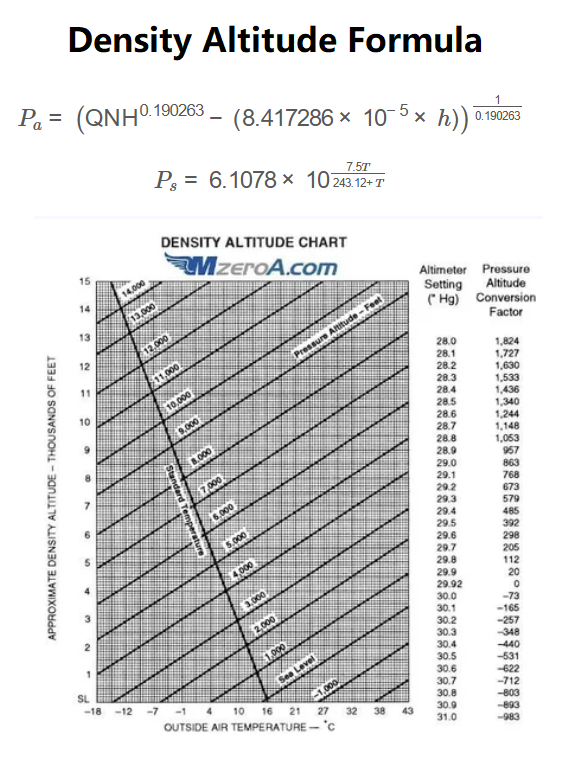
Formulas: \[ P_a = \left( \text{QNH}^{0.190263} - (8.417286 \times 10^{-5} \times h) \right)^{\frac{1}{0.190263}} \] \[ P_s = 6.1078 \times 10^{\frac{7.5T}{243.12 + T}} \] If using dew point: \[ P_v = 6.1078 \times 10^{\frac{7.5 \times \text{dew point}}{243.12 + \text{dew point}}} \] If using relative humidity: \[ P_v = P_s \times \frac{\text{RH}}{100} \] \[ P_d = P_a - (P_v \times 100) \] \[ \rho = \left( \frac{P_d}{R_d T} \right) + \left( \frac{P_v \times 100}{R_v T} \right) \] \[ \text{Relative Density} = \frac{\rho}{1.225} \] \[ H = 44.3308 - 42.2665 \times \rho^{0.234969} \] where:

\( P_a \): Absolute pressure (Pa, bar, psi, at, atm, Torr, hPa, kPa, lb/ft², mmHg, inHg)
\( P_s \): Saturation vapor pressure (hPa)
\( P_v \): Actual vapor pressure (hPa)
\( P_d \): Dry air pressure (Pa)
\( \rho \): Air density (kg/m³, g/m³, lb/ft³)
\( \text{Relative Density} \): Ratio of air density to ISA standard density (dimensionless)
\( H \): Density altitude (km, m, ft, mi)
\( \text{QNH} \): Altimeter setting (hPa, inHg, Pa, bar, psi, at, atm, Torr, kPa, lb/ft², mmHg)
\( h \): Station elevation (m, km, ft, mi)
\( T \): Air temperature (K, °C, °F)
\( \text{dew point} \): Dew point temperature (K, °C, °F)
\( \text{RH} \): Relative humidity (%)
\( R_d \): Specific gas constant for dry air, 287.058 J/(kg·K)
\( R_v \): Specific gas constant for water vapor, 461.495 J/(kg·K)

Unit Conversions:

Temperature (Air Temperature, Dew Point):
- 1 °C = T + 273.15 K
- 1 °F = (T - 32) × 5/9 + 273.15 K
- 1 K = 1 K
Pressure (Altimeter Setting, Absolute Pressure):
- 1 hPa = 100 Pa
- 1 inHg = 3386.39 Pa
- 1 Pa = 1 Pa
- 1 bar = 100000 Pa
- 1 psi = 6894.76 Pa
- 1 at = 98066.5 Pa
- 1 atm = 101325 Pa
- 1 Torr = 133.322 Pa
- 1 kPa = 1000 Pa
- 1 lb/ft² = 47.8803 Pa
- 1 mmHg = 133.322 Pa
- 1 inHg = 3386.39 Pa
Altitude (Station Elevation, Density Altitude):
- 1 m = 1 m
- 1 km = 1000 m
- 1 ft = 0.3048 m
- 1 mi = 1609.34 m
Air Density (\( \rho \)):
- 1 kg/m³ = 1 kg/m³
- 1 g/m³ = 0.001 kg/m³
- 1 lb/ft³ = 16.0185 kg/m³

Steps:

Enter the air temperature in °C, °F, or K (default is 25°C, step size 0.00001).
Select the humidity input type (dew point or relative humidity).
If using dew point, enter the dew point in °C, °F, or K (default is 15°C, step size 0.00001); if using relative humidity, enter the relative humidity as a percentage (default is 50%, step size 0.00001).
Enter the altimeter setting in hPa, inHg, Pa, bar, psi, at, atm, Torr, kPa, lb/ft², or mmHg (default is 1013.25 hPa, step size 0.00001).
Enter the station elevation in m, km, ft, or mi (default is 0 m, step size 0.00001).
Convert temperature to Kelvin (K) and Celsius (°C), altimeter setting to Pa, and elevation to meters.
Calculate the absolute pressure (\( P_a \)) using the altimeter setting and elevation.
Calculate the saturation vapor pressure (\( P_s \)) using the air temperature.
Calculate the actual vapor pressure (\( P_v \)) using either the dew point or relative humidity.
Calculate the dry air pressure (\( P_d \)) by subtracting the vapor pressure from the absolute pressure.
Calculate the air density (\( \rho \)) using the dry air and vapor pressures.
Calculate the relative density by dividing the air density by the ISA standard density (1.225 kg/m³).
Calculate the density altitude using the air density.
Convert the results to the selected units and display them, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.

3. Importance of Density Altitude Calculation

Calculating density altitude and related parameters is crucial for:

Aviation: Density altitude affects aircraft performance, including lift, engine power, and takeoff distance. Pilots need this information to ensure safe operations, especially at high elevations or in warm, humid conditions.
Meteorology: Understanding air density and pressure variations helps in weather forecasting and studying atmospheric conditions.
Engineering: Air density impacts the performance of systems like HVAC, wind turbines, and engines, requiring accurate calculations for design and operation.

4. Using the Calculator

Examples:

Example 1: Calculate the air density, relative density, absolute pressure, and density altitude with a temperature of 25°C, dew point of 15°C, altimeter setting of 1013.25 hPa, and station elevation of 0 m, with air density in kg/m³, absolute pressure in Pa, and density altitude in ft:
- Enter Temperature = 25 °C, convert to K: \( 25 + 273.15 = 298.15 \, \text{K} \), and Celsius: \( 25 \, \text{°C} \).
- Enter Dew Point = 15 °C.
- Enter Altimeter Setting = 1013.25 hPa, convert to Pa: \( 1013.25 \times 100 = 101325 \, \text{Pa} \).
- Enter Station Elevation = 0 m.
- Absolute pressure: \( P_a = \left( 101325^{0.190263} - (8.417286 \times 10^{-5} \times 0) \right)^{\frac{1}{0.190263}} = 101325 \, \text{Pa} \).
- Saturation vapor pressure: \( P_s = 6.1078 \times 10^{\frac{7.5 \times 25}{243.12 + 25}} = 31.6829 \, \text{hPa} \).
- Actual vapor pressure: \( P_v = 6.1078 \times 10^{\frac{7.5 \times 15}{243.12 + 15}} = 17.0546 \, \text{hPa} \).
- Dry air pressure: \( P_d = 101325 - (17.0546 \times 100) = 99619.54 \, \text{Pa} \).
- Air density: \( \rho = \left( \frac{99619.54}{287.058 \times 298.15} \right) + \left( \frac{17.0546 \times 100}{461.495 \times 298.15} \right) = 1.1650 + 0.0124 = 1.1774 \, \text{kg/m}^3 \).
- Relative density: \( \frac{1.1774}{1.225} = 0.9611 \).
- Density altitude: \( H = 44.3308 - 42.2665 \times 1.1774^{0.234969} = 44.3308 - 41.6657 = 2.6651 \, \text{km} \).
- Convert to ft: \( 2.6651 \times 3280.84 = 8744.77 \).
- Result: \( \rho = 1.1774 \, \text{kg/m}^3 \), Relative Density = 0.9611, \( P_a = 101325.0000 \, \text{Pa} \), Density Altitude = 8744.7655 ft.
Example 2: Calculate the air density, relative density, absolute pressure, and density altitude with a temperature of 86°F, relative humidity of 50%, altimeter setting of 29.92 inHg, and station elevation of 1000 ft, with air density in lb/ft³, absolute pressure in hPa, and density altitude in m:
- Enter Temperature = 86 °F, convert to °C: \( (86 - 32) \times 5/9 = 30 \, \text{°C} \), then to K: \( 30 + 273.15 = 303.15 \, \text{K} \).
- Enter Relative Humidity = 50%.
- Enter Altimeter Setting = 29.92 inHg, convert to Pa: \( 29.92 \times 3386.39 = 101283.99 \, \text{Pa} \).
- Enter Station Elevation = 1000 ft, convert to m: \( 1000 \times 0.3048 = 304.8 \, \text{m} \).
- Absolute pressure: \( P_a = \left( 101283.99^{0.190263} - (8.417286 \times 10^{-5} \times 304.8) \right)^{\frac{1}{0.190263}} = 97923.48 \, \text{Pa} \).
- Convert to hPa: \( 97923.48 \times 0.01 = 979.23 \).
- Saturation vapor pressure: \( P_s = 6.1078 \times 10^{\frac{7.5 \times 30}{243.12 + 30}} = 42.466 \, \text{hPa} \).
- Actual vapor pressure: \( P_v = 42.466 \times \frac{50}{100} = 21.233 \, \text{hPa} \).
- Dry air pressure: \( P_d = 97923.48 - (21.233 \times 100) = 95800.18 \, \text{Pa} \).
- Air density: \( \rho = \left( \frac{95800.18}{287.058 \times 303.15} \right) + \left( \frac{21.233 \times 100}{461.495 \times 303.15} \right) = 1.1012 + 0.0152 = 1.1164 \, \text{kg/m}^3 \).
- Convert to lb/ft³: \( 1.1164 \times 62.428 = 69.6988 \).
- Relative density: \( \frac{1.1164}{1.225} = 0.9113 \).
- Density altitude: \( H = 44.3308 - 42.2665 \times 1.1164^{0.234969} = 44.3308 - 41.1895 = 3.1413 \, \text{km} \).
- Convert to m: \( 3.1413 \times 1000 = 3141.30 \).
- Result: \( \rho = 69.6988 \, \text{lb/ft}^3 \), Relative Density = 0.9113, \( P_a = 979.2348 \, \text{hPa} \), Density Altitude = 3141.3000 m.

5. Frequently Asked Questions (FAQ)

Q: What is density altitude?
A: Density altitude is the altitude in the International Standard Atmosphere (ISA) where the air density matches the current conditions. It reflects how the aircraft "feels" the atmosphere, impacting performance metrics like lift and engine power.

Q: Why are both dew point and relative humidity options provided?
A: Dew point and relative humidity both describe the moisture content of the air. Providing both options allows users to input the parameter they know, as they can be interconverted using the saturation vapor pressure. Dew point is often more precise for low humidity levels.

Q: How does humidity affect air density and density altitude?
A: Moist air is less dense than dry air because water vapor molecules are lighter than nitrogen and oxygen. Higher humidity increases the vapor pressure, reducing the air density and thus increasing the density altitude, which can degrade aircraft performance.