Delta-to-Wye Conversion Calculator

Delta Resistance \( R_a \): ⓘ

Delta Resistance \( R_b \): ⓘ

Delta Resistance \( R_c \): ⓘ

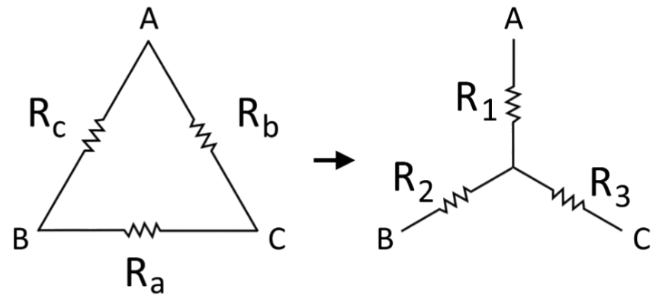
1. What is Delta-to-Wye Conversion?

Definition: Delta-to-Wye (Δ-to-Y) conversion is a technique used in electrical engineering to transform a delta (triangle) configuration of resistors into an equivalent wye (star) configuration, or vice versa. This simplifies circuit analysis in certain network topologies.

Purpose: It is used to simplify complex circuits, especially in three-phase systems, filters, and impedance matching networks, making it easier to calculate equivalent resistances.

2. How Does the Calculator Work?

The calculator uses the following formulas to compute the wye resistances:

\[ R_1 = \frac{R_b \cdot R_c}{R_a + R_b + R_c} \]

\[ R_2 = \frac{R_a \cdot R_c}{R_a + R_b + R_c} \]

\[ R_3 = \frac{R_a \cdot R_b}{R_a + R_b + R_c} \]

Where:

\( R_a, R_b, R_c \): Resistances in the delta configuration (converted to ohms)
\( R_1, R_2, R_3 \): Equivalent resistances in the wye configuration (ohms)

Steps:

Enter the delta resistances \( R_a \), \( R_b \), and \( R_c \), and select their units (ohms, kΩ, MΩ).
Click "Calculate" to compute the equivalent wye resistances \( R_1 \), \( R_2 \), and \( R_3 \).
Results are displayed in ohms.

3. Importance of Delta-to-Wye Conversion

This conversion is essential for:

Circuit Simplification: Converts complex delta networks into simpler wye networks for easier analysis.
Three-Phase Systems: Facilitates analysis of balanced or unbalanced loads in power systems.
Impedance Matching: Helps in designing circuits where equivalent impedances need to be adjusted.

4. Using the Calculator

Examples:

Example 1: Equal Resistances
- \( R_a = 120 \, \text{ohms}, R_b = 120 \, \text{ohms}, R_c = 120 \, \text{ohms} \)
- Denominator: \( 120 + 120 + 120 = 360 \)
- \( R_1 = \frac{120 \times 120}{360} = 40.0000 \, \text{ohms} \)
- \( R_2 = \frac{120 \times 120}{360} = 40.0000 \, \text{ohms} \)
- \( R_3 = \frac{120 \times 120}{360} = 40.0000 \, \text{ohms} \)
Example 2: Different Units
- \( R_a = 1 \, \text{kΩ}, R_b = 1500 \, \text{ohms}, R_c = 0.002 \, \text{MΩ} \)
- Convert: \( R_a = 1000 \, \text{ohms}, R_b = 1500 \, \text{ohms}, R_c = 2000 \, \text{ohms} \)
- Denominator: \( 1000 + 1500 + 2000 = 4500 \)
- \( R_1 = \frac{1500 \times 2000}{4500} = 666.6667 \, \text{ohms} \)
- \( R_2 = \frac{1000 \times 2000}{4500} = 444.4444 \, \text{ohms} \)
- \( R_3 = \frac{1000 \times 1500}{4500} = 333.3333 \, \text{ohms} \)
Example 3: Small Values
- \( R_a = 0.0100 \, \text{ohms}, R_b = 0.0200 \, \text{ohms}, R_c = 0.0300 \, \text{ohms} \)
- Denominator: \( 0.0100 + 0.0200 + 0.0300 = 0.0600 \)
- \( R_1 = \frac{0.0200 \times 0.0300}{0.0600} = 0.0100 \, \text{ohms} \)
- \( R_2 = \frac{0.0100 \times 0.0300}{0.0600} = 0.0050 \, \text{ohms} \)
- \( R_3 = \frac{0.0100 \times 0.0200}{0.0600} = 0.0033 \, \text{ohms} \)

5. Frequently Asked Questions (FAQ)

Q: What is the difference between delta and wye configurations?
A: A delta configuration forms a closed loop (triangle) with three resistors, while a wye configuration has three resistors connected at a common node (star). They are electrically equivalent but used in different contexts for simplification.

Q: Why is delta-to-wye conversion useful?
A: It simplifies circuit analysis by transforming a delta network into a wye network, which is often easier to handle in series-parallel combinations or three-phase systems.

Q: How does unit conversion work in the calculator?
A: The calculator converts all resistance inputs to ohms before performing calculations. For example, 1 kΩ = 1000 ohms, and 1 MΩ = 1,000,000 ohms. Results are always displayed in ohms.