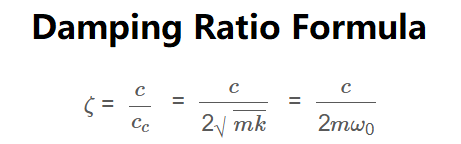Damping Ratio Calculator

Method:

Damping Coefficient (\( c \)) (Ns/m):

Suspended Mass (\( m \)):

Spring Constant (\( k \)):

Damping Coefficient (\( c \)) (Ns/m):

Suspended Mass (\( m \)):

Natural Angular Frequency (\( \omega_0 \)):

Damping Coefficient (\( c \)) (Ns/m):

Critical Damping Coefficient (\( c_c \)) (Ns/m):

1. What is a Damping Ratio Calculator?

Definition: This calculator computes the damping ratio (\(\zeta\)) of a damped harmonic oscillator, which indicates the level of damping in the system relative to critical damping.

Purpose: It is used in physics and engineering to analyze the behavior of oscillatory systems, such as springs, pendulums, or mechanical structures, to determine whether they are underdamped (\(\zeta < 1\)), critically damped (\(\zeta = 1\)), or overdamped (\(\zeta > 1\)).

2. How Does the Calculator Work?

The calculator supports three methods to calculate the damping ratio:

1. Using Critical Damping Coefficient: \[ \zeta = \frac{c}{c_c} \] 2. Using Damping Coefficient, Mass, and Spring Constant: \[ \zeta = \frac{c}{2\sqrt{mk}} \] 3. Using Damping Coefficient, Mass, and Natural Angular Frequency: \[ \zeta = \frac{c}{2m\omega_0} \] Where:

\( \zeta \): Damping ratio (dimensionless)
\( c \): Damping coefficient (Ns/m)
\( c_c \): Critical damping coefficient (Ns/m)
\( m \): Suspended mass (mg, g, dag, kg, oz, lb, st, Earth)
\( k \): Spring constant (N/m, kN/m, lbf/in, lbf/ft, dyn/cm, kips/ft, kips/in)
\( \omega_0 \): Natural angular frequency (rad/s, rpm, Hz)

Unit Conversions:

Damping Coefficient (\( c \)): Ns/m
Critical Damping Coefficient (\( c_c \)): Ns/m
Mass (\( m \)): mg (1 mg = 0.000001 kg), g (1 g = 0.001 kg), dag (1 dag = 0.01 kg), kg, oz (1 oz = 0.028349523125 kg), lb (1 lb = 0.45359237 kg), st (1 st = 6.35029318 kg), Earth (1 Earth = 5.972 × 10²⁴ kg)
Spring Constant (\( k \)): N/m, kN/m (1 kN/m = 1000 N/m), lbf/in (1 lbf/in = 175.126835 N/m), lbf/ft (1 lbf/ft = 14.5939029 N/m), dyn/cm (1 dyn/cm = 0.001 N/m), kips/ft (1 kips/ft = 14593.9029 N/m), kips/in (1 kips/in = 175126.835 N/m)
Natural Angular Frequency (\( \omega_0 \)): rad/s, rpm (1 rpm = \( \frac{2\pi}{60} \) rad/s ≈ 0.104719755 rad/s), Hz (1 Hz = \( 2\pi \) rad/s ≈ 6.283185307 rad/s)
Damping Ratio (\( \zeta \)): Dimensionless

Steps:

Select the calculation method.
Enter the required values and select their units.
Convert the mass to kg, spring constant to N/m, and natural angular frequency to rad/s for calculations.
Calculate the damping ratio using the selected formula.
Display the result, using scientific notation for values less than 0.001, otherwise with 3 decimal places.

3. Importance of Damping Ratio Calculation

Calculating the damping ratio is crucial for:

Engineering Design: Ensuring mechanical systems (e.g., suspensions, buildings) have appropriate damping to prevent excessive oscillations.
Physics Education: Understanding the behavior of damped harmonic oscillators.
Vibration Control: Optimizing damping to reduce vibrations in machinery and structures.

4. Using the Calculator

Examples:

Example 1 (Critical Damping Coefficient): For \( c = 15 \, \text{Ns/m} \), \( c_c = 22 \, \text{Ns/m} \):
- Damping Ratio: \( \zeta = \frac{15}{22} = 0.682 \)
Example 2 (Spring Constant): For \( c = 15 \, \text{Ns/m} \), \( m = 22 \, \text{kg} \), \( k = 12 \, \text{N/m} \):
- Damping Ratio: \( \zeta = \frac{15}{2 \sqrt{22 \times 12}} = \frac{15}{2 \sqrt{264}} = \frac{15}{2 \times 16.248} = 0.462 \)
Example 3 (Natural Angular Frequency): For \( c = 15 \, \text{Ns/m} \), \( m = 22 \, \text{kg} \), \( \omega_0 = 22 \, \text{rad/s} \):
- Damping Ratio: \( \zeta = \frac{15}{2 \times 22 \times 22} = \frac{15}{968} = 0.015 \)
Example 4 (Different Units): For \( c = 0.001 \, \text{Ns/m} \), \( m = 1 \, \text{g} \), \( k = 0.01 \, \text{kN/m} \):
- Convert: \( m = 1 \times 0.001 = 0.001 \, \text{kg} \), \( k = 0.01 \times 1000 = 10 \, \text{N/m} \)
- Damping Ratio: \( \zeta = \frac{0.001}{2 \sqrt{0.001 \times 10}} = \frac{0.001}{2 \sqrt{0.01}} = \frac{0.001}{2 \times 0.1} = 0.005 \)
Example 5 (Different Units): For \( c = 0.001 \, \text{Ns/m} \), \( m = 1 \, \text{g} \), \( \omega_0 = 60 \, \text{rpm} \):
- Convert: \( m = 1 \times 0.001 = 0.001 \, \text{kg} \), \( \omega_0 = 60 \times \frac{2\pi}{60} = 6.283185307 \, \text{rad/s} \)
- Damping Ratio: \( \zeta = \frac{0.001}{2 \times 0.001 \times 6.283185307} = \frac{0.001}{0.012566} \approx 0.080 \)

5. Frequently Asked Questions (FAQ)

Q: What is the damping ratio?
A: The damping ratio (\(\zeta\)) is a dimensionless quantity that describes the level of damping in a harmonic oscillator relative to critical damping. It determines whether the system is underdamped (\(\zeta < 1\)), critically damped (\(\zeta = 1\)), or overdamped (\(\zeta > 1\)).

Q: What is the critical damping coefficient?
A: The critical damping coefficient (\(c_c\)) is the damping coefficient at which the system achieves critical damping, where oscillations are suppressed as quickly as possible without overshooting. It can be calculated as \( c_c = 2\sqrt{mk} \) or \( c_c = 2m\omega_0 \).

Q: What does a damping ratio less than 1 indicate?
A: A damping ratio less than 1 (\(\zeta < 1\)) indicates an underdamped system, where the system oscillates with decreasing amplitude over time before coming to rest.