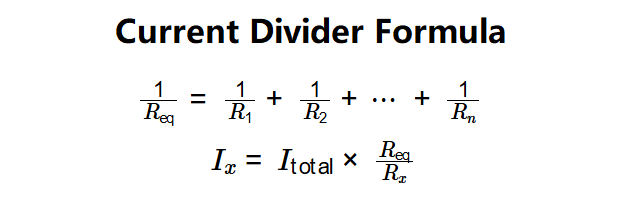Current Divider Calculator

Total Current (\( I_{\text{total}} \)):

Number of Resistors:

Current through \( R_{1} \) (\( I_{1} \)):

Current through \( R_{2} \) (\( I_{2} \)):

1. What is Current Divider Calculator?

Definition: This calculator computes the current through each branch of a parallel resistive circuit given the total current and the resistance of each branch.

Purpose: It is used in electronics to analyze how current divides in parallel circuits, which is essential for designing circuits like power distribution networks, LED arrays, or any system where components are connected in parallel.

2. How Does the Calculator Work?

The calculator uses the current divider rule for a parallel resistive circuit:

Equivalent Resistance: \( \frac{1}{R_{\text{eq}}} = \frac{1}{R_1} + \frac{1}{R_2} + \cdots + \frac{1}{R_n} \)
Current through branch \( R_x \): \( I_x = I_{\text{total}} \times \frac{R_{\text{eq}}}{R_x} \)

Where:

\( I_{\text{total}} \): Total current entering the parallel circuit (A)
\( R_{\text{eq}} \): Equivalent resistance of the parallel circuit (Ω)
\( R_x \): Resistance of the branch (Ω)
\( I_x \): Current through the branch (A)

Steps:

Select the number of resistors (branches).
Enter the total current (\( I_{\text{total}} \)) and the resistance of each branch with their units.
Convert all inputs to base units (A, Ω).
Calculate the equivalent resistance of the parallel circuit.
Compute the current through each branch using the current divider rule.
Convert the results to the selected output unit.
Display the results with 4 decimal places.

3. Importance of Current Divider Calculation

Calculating how current divides in a parallel circuit is crucial for:

Circuit Design: Ensuring each component in a parallel circuit receives the appropriate current, such as in LED lighting or resistor networks.
Power Distribution: Managing how current is distributed in power supplies or battery management systems.
Safety: Preventing overcurrent in specific branches by selecting appropriate resistor values.

4. Using the Calculator

Example 1: Calculate the current through each branch of a parallel circuit with four resistors (\( R_1 = 20 \, \Omega \), \( R_2 = 40 \, \Omega \), \( R_3 = 80 \, \Omega \), \( R_4 = 100 \, \Omega \)) and a total current of 1 A:

Total Current (\( I_{\text{total}} \)): 1 A
Resistances: \( R_1 = 20 \, \Omega \), \( R_2 = 40 \, \Omega \), \( R_3 = 80 \, \Omega \), \( R_4 = 100 \, \Omega \)
Equivalent Resistance: \( \frac{1}{R_{\text{eq}}} = \frac{1}{20} + \frac{1}{40} + \frac{1}{80} + \frac{1}{100} = 0.05 + 0.025 + 0.0125 + 0.01 = 0.0975 \, \Omega^{-1} \)
\( R_{\text{eq}} = \frac{1}{0.0975} \approx 10.2564 \, \Omega \)
Current through each branch:
\( I_1 = 1 \times \frac{10.2564}{20} \approx 0.5128 \, \text{A} \)
\( I_2 = 1 \times \frac{10.2564}{40} \approx 0.2564 \, \text{A} \)
\( I_3 = 1 \times \frac{10.2564}{80} \approx 0.1282 \, \text{A} \)
\( I_4 = 1 \times \frac{10.2564}{100} \approx 0.1026 \, \text{A} \)
Result: \( I_1 = 0.5128 \, \text{A} \), \( I_2 = 0.2564 \, \text{A} \), \( I_3 = 0.1282 \, \text{A} \), \( I_4 = 0.1026 \, \text{A} \)

Example 2: Calculate the current through each branch of a parallel circuit with two resistors (\( R_1 = 10 \, \Omega \), \( R_2 = 10 \, \Omega \)) and a total current of 2 A:

Total Current (\( I_{\text{total}} \)): 2 A
Resistances: \( R_1 = 10 \, \Omega \), \( R_2 = 10 \, \Omega \)
Equivalent Resistance: \( \frac{1}{R_{\text{eq}}} = \frac{1}{10} + \frac{1}{10} = 0.2 \, \Omega^{-1} \)
\( R_{\text{eq}} = \frac{1}{0.2} = 5 \, \Omega \)
Current through each branch:
\( I_1 = 2 \times \frac{5}{10} = 1 \, \text{A} \)
\( I_2 = 2 \times \frac{5}{10} = 1 \, \text{A} \)
Result: \( I_1 = 1.0000 \, \text{A} \), \( I_2 = 1.0000 \, \text{A} \)

5. Frequently Asked Questions (FAQ)

Q: Why does current divide in a parallel circuit?
A: In a parallel circuit, the voltage across each branch is the same, but the current divides based on the resistance of each branch. According to Ohm’s Law (\( I = V/R \)), a lower resistance allows more current to flow through that branch.

Q: Can this calculator be used for series circuits?
A: No, this calculator is designed for parallel circuits. In a series circuit, the current is the same through all components, and you would need a voltage divider calculator instead.

Q: How does current division work with inductive or capacitive circuits?
A: For inductive or capacitive circuits, you need to consider impedance (which includes reactance) instead of just resistance. This calculator focuses on resistive circuits, but the principle can be extended to AC circuits by using impedance in place of resistance.