Cubic Block Inclined Plane Calculator

Mass (m):

Angle of Incline (θ):

Friction Coefficient (f):

Height (H):

Resulting Force (F):

Length (L):

Acceleration (a):

Sliding Time (t):

Final Velocity (v):

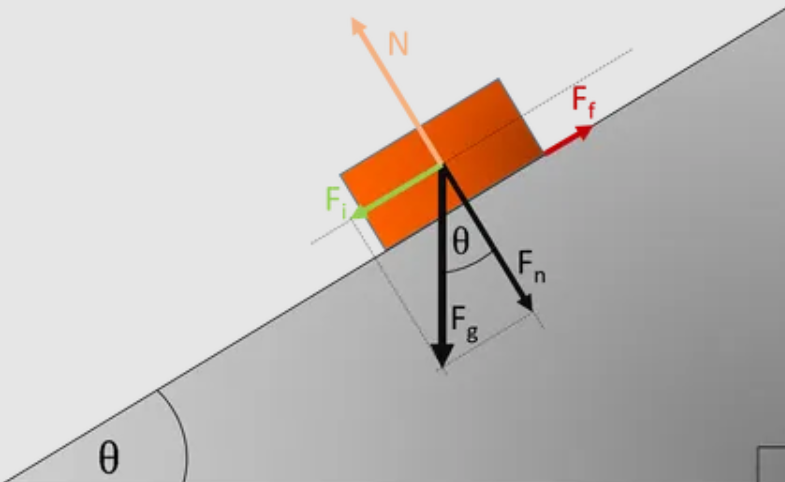
1. What is a Cubic Block Inclined Plane Calculator?

Definition: This calculator determines the forces, acceleration, sliding time, final velocity, and energy loss of a cubic block sliding down an inclined plane, accounting for gravity and friction.

Purpose: It is used in physics to analyze the motion of objects on inclined planes, such as a block sliding down a ramp, aiding in understanding mechanics principles.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Length of Incline: \[ L = \frac{H}{\sin \theta} \] Resulting Force: \[ F = F_g \times (\sin \theta - f \cos \theta), \quad \text{where} \quad F_g = m \times g \] Acceleration: \[ a = \frac{F}{m} \] Sliding Time: \[ t = \sqrt{\frac{2 L}{a}} \quad (\text{if } v_0 = 0) \] Final Velocity: \[ v = a \times t \quad (\text{if } v_0 = 0) \] Energy Loss: \[ \Delta E = F_f \times L, \quad \text{where} \quad F_f = f \times F_n, \quad F_n = F_g \times \cos \theta \] Where:

\(L\): Length of incline (cm, m, in, ft, yd, km, mi)
\(F\): Resulting force (N, kN, MN, GN, lbf)
\(a\): Acceleration (m/s², g, ft/s²)
\(t\): Sliding time (sec, min, hrs)
\(v\): Final velocity (m/s, km/h, ft/s, mph, kn, ft/min)
\(\Delta E\): Energy loss (J, kJ, MJ, Wh, kWh, ft-lb, kcal)
\(m\): Mass (mg, g, kg, oz, lb)
\(H\): Height of incline (cm, m, in, ft, yd, km, mi)
\(\theta\): Angle of incline (degrees, radians)
\(f\): Friction coefficient (unitless)
\(g\): Acceleration due to gravity (\(9.81 \, \text{m/s}^2\))

Unit Conversions:

Mass Units (m): mg, g, kg, oz, lb
Angle Units (θ): degrees, radians
Height/Length Units (H, L): cm, m, in, ft, yd, km, mi
Force Units (F): N, kN, MN, GN, lbf
Acceleration Units (a): m/s², g, ft/s²
Time Units (t): sec, min, hrs
Velocity Units (v): m/s, km/h, ft/s, mph, kn, ft/min
Energy Units (ΔE): J, kJ, MJ, Wh, kWh, ft-lb, kcal

Steps:

Enter the mass (m), selecting the unit (mg, g, kg, oz, lb)
Enter the angle of incline (θ), selecting the unit (degrees, radians)
Enter the friction coefficient (f)
Enter the height of the incline (H), selecting the unit (cm, m, in, ft, yd, km, mi)
Convert all inputs to SI units (kg, radians, m)
Calculate the length of the incline, resulting force, acceleration, sliding time, final velocity, and energy loss
Select the desired units for the results and view the converted values

3. Importance of Inclined Plane Calculation

Calculating the motion on an inclined plane is crucial for:

Physics Education: Understanding the effects of gravity, friction, and inclined surfaces on motion.
Engineering Design: Designing ramps, conveyor belts, or slides where objects move under gravity.
Safety Analysis: Predicting the speed and time of descent to ensure safety in scenarios like landslides or vehicle skids.

4. Using the Calculator

Examples:

Example 1: For a mass \(m = 22.56 \, \text{kg}\), angle \(\theta = 30^\circ\), friction coefficient \(f = 0\), height \(H = 12.33 \, \text{m}\):
- Length = \(\frac{12.33}{\sin(30^\circ)} = 24.66 \, \text{m}\)
- Gravitational force = \(22.56 \times 9.81 = 221.31 \, \text{N}\)
- Force parallel = \(221.31 \times \sin(30^\circ) = 110.66 \, \text{N}\)
- Normal force = \(221.31 \times \cos(30^\circ) = 191.68 \, \text{N}\)
- Frictional force = \(0 \times 191.68 = 0 \, \text{N}\)
- Resulting force = \(110.66 - 0 = 110.66 \, \text{N}\)
- Acceleration = \(110.66 / 22.56 = 4.903 \, \text{m/s}^2\)
- Time = \(\sqrt{\frac{2 \times 24.66}{4.903}} = 3.172 \, \text{s}\)
- Final velocity = \(4.903 \times 3.172 = 15.55 \, \text{m/s}\)
- Energy loss = \(0 \times 24.66 = 0 \, \text{J}\)
Example 2: For a mass \(m = 1 \, \text{lb}\), angle \(\theta = 0.5 \, \text{radians}\), friction coefficient \(f = 0.0001\), height \(H = 2 \, \text{ft}\):
- Mass in kg = \(1 \times 0.453592 = 0.453592 \, \text{kg}\)
- Height in m = \(2 \times 0.3048 = 0.6096 \, \text{m}\)
- Length in m = \(\frac{0.6096}{\sin(0.5)} = 1.263 \, \text{m}\)
- Gravitational force = \(0.453592 \times 9.81 = 4.45 \, \text{N}\)
- Force parallel = \(4.45 \times \sin(0.5) = 2.14 \, \text{N}\)
- Normal force = \(4.45 \times \cos(0.5) = 4.04 \, \text{N}\)
- Frictional force = \(0.0001 \times 4.04 = 0.000404 \, \text{N}\)
- Resulting force = \(2.14 - 0.000404 = 2.14 \, \text{N}\)
- Acceleration = \(2.14 / 0.453592 = 4.72 \, \text{m/s}^2\)
- Time = \(\sqrt{\frac{2 \times 1.263}{4.72}} = 0.732 \, \text{s}\)
- Final velocity = \(4.72 \times 0.732 = 3.46 \, \text{m/s}\)
- Energy loss = \(0.000404 \times 1.263 = 0.00051 \, \text{J}\)
- In kJ = \(0.00051 \times 0.001 = 0.00000051 \, \text{kJ} = 5.10 \times 10^{-7} \, \text{kJ}\) (scientific notation)

5. Frequently Asked Questions (FAQ)

Q: What is an inclined plane?
A: An inclined plane is a flat surface tilted at an angle, used to raise or lower objects with less force than lifting vertically, such as a ramp.

Q: Why does friction affect the motion?
A: Friction opposes the motion along the incline, reducing the resulting force and acceleration, calculated as \( F_f = f \times F_n \).

Q: What happens if the friction is too high?
A: If the frictional force exceeds the parallel component of gravity (\( F_f \geq F_i \)), the block will not slide, resulting in zero acceleration and infinite sliding time.