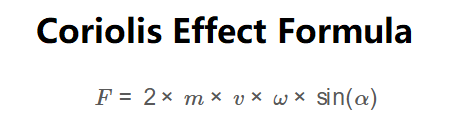1. What is a Coriolis Effect Calculator?
Definition: This calculator computes the Coriolis force and associated acceleration experienced by a moving object on a rotating body (Earth) due to the Coriolis effect.
Purpose: It is used in physics and meteorology to analyze the effect of Earth's rotation on moving objects, such as winds, ocean currents, or projectiles.
2. How Does the Calculator Work?
The calculator uses the following formulas:
Angular Velocity (\( \omega \)) for Earth:
\[
\omega = \frac{2\pi}{24 \times 3600} \approx 0.0000727 \, \text{rad/s}
\]
Coriolis Force:
\[
F = 2 \times m \times v \times \omega \times \sin(\alpha)
\]
Coriolis Acceleration:
\[
a = \frac{F}{m} = 2 \times v \times \omega \times \sin(\alpha)
\]
Where:
- \( F \): Coriolis force (N, kN, pdl, lbf)
- \( m \): Mass (mg, g, dag, kg, oz, lb, st, Earth)
- \( v \): Velocity (m/s, km/h, ft/s, mph, km/s, mi/s)
- \( \omega \): Angular velocity of Earth (rad/s, calculated as 0.0000727 rad/s)
- \( \alpha \): Latitude (degrees)
- \( a \): Coriolis acceleration (m/s², g)
Unit Conversions:
- Mass (\( m \)): mg (1 mg = 0.000001 kg), g (1 g = 0.001 kg), dag (1 dag = 0.01 kg), kg, oz (1 oz = 0.028349523125 kg), lb (1 lb = 0.45359237 kg), st (1 st = 6.35029318 kg), Earth (1 Earth = 5.972 × 10²⁴ kg)
- Velocity (\( v \)): m/s, km/h (1 km/h = \( \frac{1000}{3600} \) m/s ≈ 0.277777778 m/s), ft/s (1 ft/s = 0.3048 m/s), mph (1 mph = 0.44704 m/s), km/s (1 km/s = 1000 m/s), mi/s (1 mi/s = 1609.344 m/s)
- Angular Velocity (\( \omega \)): rad/s (calculated as 0.0000727 rad/s for Earth)
- Latitude (\( \alpha \)): degrees
- Coriolis Force (\( F \)): N, kN (1 kN = 1000 N), pdl (1 N = 7.233013851209894 pdl), lbf (1 N = 0.224808943 lbf)
- Coriolis Acceleration (\( a \)): m/s², g (1 g = 9.80665 m/s²)
Steps:
- Enter the mass, velocity, and latitude, and select their units.
- Convert the mass to kg and velocity to m/s for calculations.
- Calculate Earth's angular velocity (\( \omega \)) as \( \frac{2\pi}{24 \times 3600} \).
- Convert the latitude to radians for the sine function.
- Calculate the Coriolis force and acceleration.
- Convert the force and acceleration to the selected units.
- Display the results, using scientific notation for values less than 0.001, otherwise with 3 decimal places.
3. Importance of Coriolis Effect Calculation
Calculating the Coriolis effect is crucial for:
- Meteorology: Understanding the deflection of winds and ocean currents due to Earth's rotation.
- Physics Education: Studying the effects of non-inertial reference frames.
- Navigation and Aviation: Accounting for the Coriolis effect in long-distance travel.
4. Using the Calculator
Examples:
- Example 1: For \( m = 1 \, \text{kg} \), \( v = 10 \, \text{m/s} \), \( \alpha = 45^\circ \), force in N, acceleration in m/s²:
- Earth's Angular Velocity: \( \omega = \frac{2\pi}{24 \times 3600} \approx 0.0000727 \, \text{rad/s} \)
- Convert: \( \alpha = 45^\circ \times \frac{\pi}{180} = 0.7854 \, \text{rad} \), \( \sin(45^\circ) = 0.7071 \)
- Coriolis Force: \( F = 2 \times 1 \times 10 \times 0.0000727 \times 0.7071 = 0.00103 \, \text{N} \)
- Coriolis Acceleration: \( a = \frac{0.00103}{1} = 0.00103 \, \text{m/s}^2 \)
- Example 2: For \( m = 500 \, \text{g} \), \( v = 36 \, \text{km/h} \), \( \alpha = 30^\circ \), force in lbf, acceleration in g:
- Earth's Angular Velocity: \( \omega = \frac{2\pi}{24 \times 3600} \approx 0.0000727 \, \text{rad/s} \)
- Convert: \( m = 500 \times 0.001 = 0.5 \, \text{kg} \), \( v = 36 \times \frac{1000}{3600} = 10 \, \text{m/s} \), \( \alpha = 30^\circ \times \frac{\pi}{180} = 0.5236 \, \text{rad} \), \( \sin(30^\circ) = 0.5 \)
- Coriolis Force: \( F = 2 \times 0.5 \times 10 \times 0.0000727 \times 0.5 = 0.0003635 \, \text{N} \), \( F = 0.0003635 \times 0.224808943 = 8.17 \times 10^{-5} \, \text{lbf} \)
- Coriolis Acceleration: \( a = \frac{0.0003635}{0.5} = 0.000727 \, \text{m/s}^2 \), \( a = \frac{0.000727}{9.80665} = 7.42 \times 10^{-5} \, \text{g} \)
- Example 3 (Zero Latitude): For \( m = 1 \, \text{mg} \), \( v = 0.1 \, \text{m/s} \), \( \alpha = 0^\circ \), force in N, acceleration in m/s²:
- Earth's Angular Velocity: \( \omega = \frac{2\pi}{24 \times 3600} \approx 0.0000727 \, \text{rad/s} \)
- Convert: \( m = 1 \times 0.000001 = 0.000001 \, \text{kg} \), \( \alpha = 0^\circ \times \frac{\pi}{180} = 0 \, \text{rad} \), \( \sin(0^\circ) = 0 \)
- Coriolis Force: \( F = 2 \times 0.000001 \times 0.1 \times 0.0000727 \times 0 = 0.000 \, \text{N} \)
- Coriolis Acceleration: \( a = \frac{0}{0.000001} = 0.000 \, \text{m/s}^2 \)
5. Frequently Asked Questions (FAQ)
Q: What is the Coriolis effect?
A: The Coriolis effect is a fictitious force experienced by objects moving in a rotating reference frame, such as on Earth, causing a deflection due to the rotation.
Q: Why is the angular velocity calculated automatically?
A: The calculator assumes the rotating body is Earth, with an angular velocity of \( \omega = \frac{2\pi}{24 \times 3600} \approx 0.0000727 \, \text{rad/s} \), since Earth completes one full rotation (2π radians) in 24 hours (86,400 seconds).
Q: How does latitude affect the Coriolis force?
A: The Coriolis force depends on \( \sin(\alpha) \), where \( \alpha \) is the latitude. At the equator (\( \alpha = 0^\circ \)), \( \sin(0) = 0 \), so the Coriolis force is zero. At the poles (\( \alpha = \pm 90^\circ \)), \( \sin(\pm 90) = \pm 1 \), so the effect is maximized.
Coriolis Effect Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back