Concave Mirror Calculator

Object Distance (p):

Radius of Curvature (r):

Object Height (h₀):

Focal Length (f):

Image Distance (q):

Magnification (m):

(unitless)

Image Height (hᵢ):

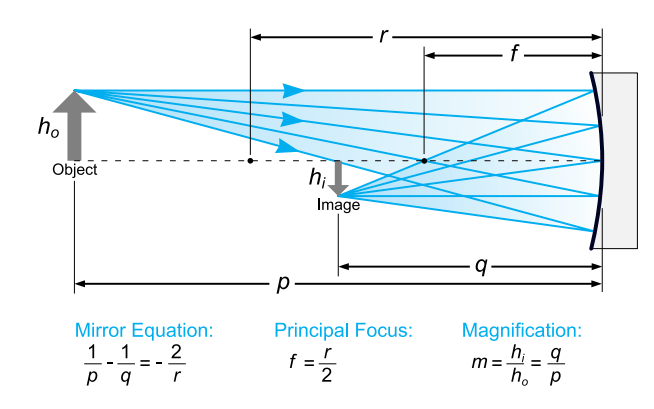
1. What is a Concave Mirror Calculator?

Definition: This calculator determines the focal length, image distance, magnification, and image height for a concave mirror based on object distance, radius of curvature, and object height.

Purpose: Assists in optics studies and applications like telescope design or medical imaging.

2. How Does the Calculator Work?

The calculator uses the following steps:

Step 1: Calculate Focal Length

\( f = \frac{r}{2} \)

Where:

\( r \): Radius of curvature

Step 2: Mirror Equation

\( \frac{1}{p} - \frac{1}{q} = -\frac{2}{r} \)

Where:

\( p \): Object distance
\( q \): Image distance

Step 3: Magnification

\( m = \frac{q}{p} \)

Where:

\( m \): Magnification

Step 4: Image Height

\( h_i = m \times h_0 \)

Where:

\( h_i \): Image height
\( h_0 \): Object height

Steps:

Enter object distance, radius of curvature, and object height with selected units (default cm).
Convert all inputs to centimeters for calculation.
Convert results back to the selected units and display with 2 decimal places.

3. Importance of Concave Mirrors

Concave mirrors are crucial for:

Optics: Used in telescopes and microscopes.
Medical Devices: Employed in dental mirrors and headlamps.
Lighting: Focus light in projectors and car headlights.

4. Using the Calculator

Example 1: p = 20 cm, r = 40 cm, h₀ = 5 cm:

Focal Length: \( f = \frac{40}{2} = 20 \) cm
Image Distance: \( \frac{1}{20} - \frac{1}{q} = -\frac{2}{40} \), \( \frac{1}{q} = \frac{1}{20} + \frac{1}{20} \), \( q = 10 \) cm
Magnification: \( m = \frac{10}{20} = 0.5 \)
Image Height: \( h_i = 0.5 \times 5 = 2.5 \) cm
Result: f = 20 cm, q = 10 cm, m = 0.5, hᵢ = 2.5 cm

5. Frequently Asked Questions (FAQ)

Q: What does magnification mean?
A: It indicates the size ratio of the image to the object.

Q: Why is focal length half the radius?
A: Due to the geometry of a spherical concave mirror.

Q: Where to find these values?
A: Refer to optics experiments or mirror specifications.