Compton Scattering Calculator

Scattering Angle (\( \theta \)):

Mass of Particle (\( m \)):

1. What is the Compton Scattering Calculator?

Definition: This calculator uses the Compton scattering equation to compute the difference in wavelength (\( \Delta \lambda \)) between the incident and scattered photons.

Purpose: It is used in quantum physics to study the interaction of photons with matter, particularly in understanding the scattering of X-rays and gamma rays by particles such as electrons.

2. How Does the Calculator Work?

The calculator uses the following equation:

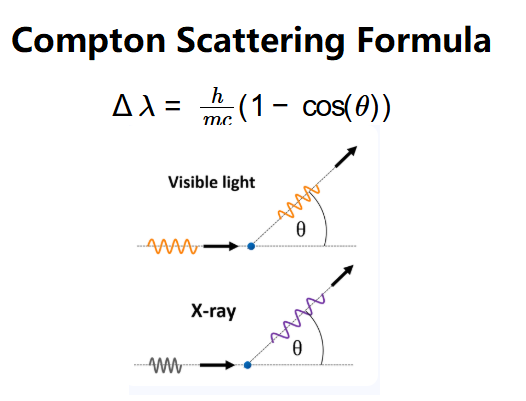
\( \Delta \lambda = \frac{h}{m c} (1 - \cos(\theta)) \)

Where:

\( \Delta \lambda \): Wavelength difference (m, cm, mm, nm, pm, or Å);
\( h \): Planck's constant (\( 6.62607 \times 10^{-34} \, \text{J·s} \));
\( m \): Mass of the particle (various units);
\( c \): Speed of light (\( 299792458 \, \text{m/s} \));
\( \theta \): Scattering angle (degrees or radians).

Steps:

Enter the scattering angle (\( \theta \)) with its unit (degrees or radians).
Enter the mass of the particle (\( m \)) with its unit.
Convert the angle to radians if necessary.
Convert the mass to kilograms.
Calculate the Compton wavelength: \( \frac{h}{m c} \).
Calculate the wavelength difference: \( \Delta \lambda = \frac{h}{m c} (1 - \cos(\theta)) \).
Convert the wavelength difference to the selected output unit and display \( \Delta \lambda \), formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Compton Scattering Calculation

Calculating the wavelength shift in Compton scattering is crucial for:

Quantum Physics: Validating the particle nature of light and the principles of quantum mechanics.
X-ray Crystallography: Understanding the scattering of X-rays by particles in materials.
Medical Imaging: Applications in radiology and understanding photon interactions in tissues.

4. Using the Calculator

Example 1: Calculate \( \Delta \lambda \) for a photon scattered by an electron at an angle:

Scattering Angle: \( \theta = 90^\circ \);
Mass: \( m = 1 \, m_e = 9.1093837 \times 10^{-31} \, \text{kg} \);
Convert to radians: \( \theta = 90 \times \frac{\pi}{180} = \frac{\pi}{2} \);
Compton wavelength: \( \frac{h}{m c} = \frac{6.62607 \times 10^{-34}}{9.1093837 \times 10^{-31} \times 299792458} \approx 2.4263 \times 10^{-12} \, \text{m} \);
Wavelength Difference: \( \Delta \lambda = 2.4263 \times 10^{-12} \times (1 - \cos(\frac{\pi}{2})) = 2.4263 \times 10^{-12} \times 1 = 2.4263 \times 10^{-12} \, \text{m} \);
Result: \( \Delta \lambda = 2.4263 \times 10^{-12} \, \text{m} \) or \( 2.4263 \, \text{nm} \).

Example 2 (Different Mass and Unit): Calculate \( \Delta \lambda \) with the following properties:

Scattering Angle: \( \theta = 180^\circ \);
Mass: \( m = 1 \, m_p = 1.6726219 \times 10^{-27} \, \text{kg} \);
Convert to radians: \( \theta = 180 \times \frac{\pi}{180} = \pi \);
Compton wavelength: \( \frac{h}{m c} = \frac{6.62607 \times 10^{-34}}{1.6726219 \times 10^{-27} \times 299792458} \approx 1.3214 \times 10^{-15} \, \text{m} \);
Wavelength Difference: \( \Delta \lambda = 1.3214 \times 10^{-15} \times (1 - \cos(\pi)) = 1.3214 \times 10^{-15} \times (1 - (-1)) = 2.6428 \times 10^{-15} \, \text{m} \);
Result: \( \Delta \lambda = 2.6428 \times 10^{-15} \, \text{m} \) or \( 0.0026 \, \text{pm} \).

5. Frequently Asked Questions (FAQ)

Q: What does a larger scattering angle mean?
A: A larger scattering angle (\( \theta \)) results in a greater wavelength shift, with the maximum shift occurring at \( \theta = 180^\circ \).

Q: Why is there no wavelength shift at \( \theta = 0^\circ \)?
A: At \( \theta = 0^\circ \), the photon continues in the same direction, so there is no energy loss, and thus no wavelength shift (\( \cos(0) = 1 \)).

Q: How does the mass of the particle affect the result?
A: A larger mass results in a smaller Compton wavelength (\( \frac{h}{m c} \)), leading to a smaller wavelength shift for the same scattering angle.