Circular Motion Calculator

Frequency (\( f \)):

Angular Velocity (\( \omega \)) (rad/s):

Speed (\( v \)):

Centripetal Acceleration (\( a \)):

1. What is a Circular Motion Calculator?

Definition: This calculator computes properties of circular motion, such as frequency, angular velocity, speed, and centripetal acceleration, given the time period and radius of the motion.

Purpose: It is used in physics to analyze objects moving in a circular path, such as satellites, amusement park rides, or particles in a centrifuge.

2. How Does the Calculator Work?

The calculator uses the following formulas:

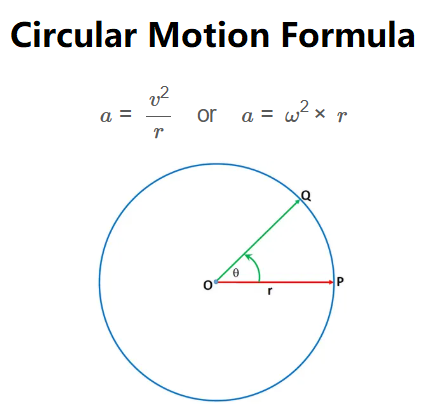
Frequency: \[ f = \frac{1}{T} \] Angular Velocity: \[ \omega = \frac{2\pi}{T} \] Speed: \[ v = \omega \times r \] Centripetal Acceleration: \[ a = \frac{v^2}{r} \quad \text{or} \quad a = \omega^2 \times r \] Where:

\( T \): Time period (sec, min, hr)
\( f \): Frequency (Hz, RPM)
\( \omega \): Angular velocity (rad/s)
\( r \): Radius (mm, cm, m, in, ft, yd)
\( v \): Speed (m/s, km/h, ft/s, mph, km/s, mi/s)
\( a \): Centripetal acceleration (m/s², g)

Unit Conversions:

Time Period (\( T \)): sec, min (1 min = 60 sec), hr (1 hr = 3600 sec)
Frequency (\( f \)): Hz, RPM (1 Hz = 60 RPM)
Angular Velocity (\( \omega \)): rad/s (radians per second)
Radius (\( r \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
Speed (\( v \)): m/s, km/h (1 m/s = 3.6 km/h), ft/s (1 m/s = 3.28084 ft/s), mph (1 m/s = 2.23694 mph), km/s (1 m/s = 0.001 km/s), mi/s (1 m/s = 0.000621371 mi/s)
Centripetal Acceleration (\( a \)): m/s², g (1 g = 9.80665 m/s²)

Steps:

Enter the time period and radius, and select their units.
Convert the time period to seconds and the radius to meters for calculations.
Calculate the frequency, angular velocity, speed, and centripetal acceleration.
Convert the frequency, speed, and acceleration to the selected units.
Display the results, using scientific notation for values less than 0.001, otherwise with specified decimal places.

3. Importance of Circular Motion Calculation

Calculating circular motion properties is crucial for:

Physics Education: Understanding the dynamics of circular motion.
Engineering: Designing systems involving rotation, such as wheels, gears, or amusement park rides.
Astronomy: Analyzing the motion of celestial bodies in orbits.

4. Using the Calculator

Examples:

Example 1: For \( T = 23 \, \text{sec} \), \( r = 23 \, \text{m} \), frequency in Hz, speed in m/s, acceleration in m/s²:
- Frequency: \( f = \frac{1}{23} = 0.04348 \, \text{Hz} \)
- Angular Velocity: \( \omega = \frac{2\pi}{23} = 0.2732 \, \text{rad/s} \)
- Speed: \( v = 0.2732 \times 23 = 6.283 \, \text{m/s} \)
- Centripetal Acceleration: \( a = \frac{(6.283)^2}{23} = 1.7165 \, \text{m/s}^2 \)
Example 2: For \( T = 2 \, \text{min} \), \( r = 50 \, \text{cm} \), frequency in RPM, speed in km/h, acceleration in g:
- Convert: \( T = 2 \times 60 = 120 \, \text{sec} \), \( r = 50 \times 0.01 = 0.5 \, \text{m} \)
- Frequency: \( f = \frac{1}{120} = 0.00833 \, \text{Hz} \), \( f = 0.00833 \times 60 = 0.50000 \, \text{RPM} \)
- Angular Velocity: \( \omega = \frac{2\pi}{120} = 0.05236 \, \text{rad/s} \)
- Speed: \( v = 0.05236 \times 0.5 = 0.02618 \, \text{m/s} \), \( v = 0.02618 \times 3.6 = 0.094 \, \text{km/h} \)
- Centripetal Acceleration: \( a = \frac{(0.02618)^2}{0.5} = 0.00137 \, \text{m/s}^2 \), \( a = \frac{0.00137}{9.80665} = 0.00014 \, \text{g} \)
Example 3 (Small Values): For \( T = 0.1 \, \text{sec} \), \( r = 1 \, \text{mm} \), frequency in Hz, speed in m/s, acceleration in m/s²:
- Convert: \( r = 1 \times 0.001 = 0.001 \, \text{m} \)
- Frequency: \( f = \frac{1}{0.1} = 10.00000 \, \text{Hz} \)
- Angular Velocity: \( \omega = \frac{2\pi}{0.1} = 62.8319 \, \text{rad/s} \)
- Speed: \( v = 62.8319 \times 0.001 = 0.063 \, \text{m/s} \)
- Centripetal Acceleration: \( a = \frac{(0.063)^2}{0.001} = 3.949 \, \text{m/s}^2 \)
Example 4: For \( T = 1 \, \text{hr} \), \( r = 1 \, \text{m} \), frequency in RPM, speed in m/s, acceleration in m/s²:
- Convert: \( T = 1 \times 3600 = 3600 \, \text{sec} \)
- Frequency: \( f = \frac{1}{3600} = 0.00028 \, \text{Hz} \), \( f = 0.00028 \times 60 = 0.01667 \, \text{RPM} \)
- Angular Velocity: \( \omega = \frac{2\pi}{3600} = 0.00175 \, \text{rad/s} \)
- Speed: \( v = 0.00175 \times 1 = 0.002 \, \text{m/s} \)
- Centripetal Acceleration: \( a = \frac{(0.002)^2}{1} = 0.000 \, \text{m/s}^2 \), display as \( 3.046 \times 10^{-6} \, \text{m/s}^2 \)

5. Frequently Asked Questions (FAQ)

Q: What is circular motion?
A: Circular motion is the movement of an object along a circular path, where the object maintains a constant distance (radius) from a central point.

Q: How is frequency related to time period?
A: Frequency (\(f\)) is the inverse of the time period (\(T\)): \( f = \frac{1}{T} \). It measures how many cycles occur per second (Hz) or per minute (RPM).

Q: What is centripetal acceleration?
A: Centripetal acceleration is the acceleration directed toward the center of the circular path, required to keep an object moving in a circle. It is calculated as \( a = \frac{v^2}{r} \) or \( a = \omega^2 \times r \).