Charles' Law Calculator

Initial Volume (\( V_1 \)):

Initial Temperature (\( T_1 \)):

Calculate:

Final Temperature (\( T_2 \)):

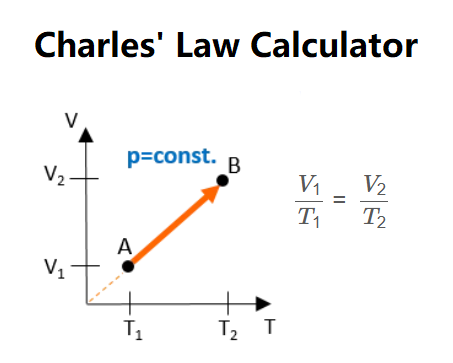
1. What is the Charles' Law Calculator?

Definition: This calculator uses Charles' Law to compute the final volume (\( V_2 \)) or final temperature (\( T_2 \)) of a gas at constant pressure, given the initial volume (\( V_1 \)), initial temperature (\( T_1 \)), and one of the final parameters. Charles' Law states that for a fixed amount of gas at constant pressure, the volume is directly proportional to its absolute temperature.

Purpose: It is used in thermodynamics to analyze the behavior of gases under changing temperature conditions, such as in hot air balloons, vehicle tires, and industrial processes involving gases.

2. How Does the Calculator Work?

The calculator uses Charles' Law:

Formula: \[ \frac{V_1}{T_1} = \frac{V_2}{T_2} \] To find the final volume: \[ V_2 = V_1 \cdot \frac{T_2}{T_1} \] To find the final temperature: \[ T_2 = T_1 \cdot \frac{V_2}{V_1} \] where:

\( V_1 \): Initial volume (mm³, cm³, in³, L, mL, ft³, yd³, m³)
\( T_1 \): Initial temperature (K, °C, °F)
\( V_2 \): Final volume (mm³, cm³, in³, L, mL, ft³, yd³, m³)
\( T_2 \): Final temperature (K, °C, °F)

Unit Conversions:

Volume (\( V_1 \), \( V_2 \)):
- 1 mm³ = \( 1 \times 10^{-9} \, \text{m}^3 \)
- 1 cm³ = \( 1 \times 10^{-6} \, \text{m}^3 \)
- 1 in³ = \( 1.63871 \times 10^{-5} \, \text{m}^3 \)
- 1 L = 0.001 m³
- 1 mL = \( 1 \times 10^{-6} \, \text{m}^3 \)
- 1 ft³ = 0.0283168 m³
- 1 yd³ = 0.764555 m³
- 1 m³ = 1 m³
Temperature (\( T_1 \), \( T_2 \)):
- Kelvin (K): No conversion needed
- Celsius (°C) to Kelvin: \( T_K = T_C + 273.15 \)
- Fahrenheit (°F) to Kelvin: \( T_K = (T_F - 32) \cdot \frac{5}{9} + 273.15 \)

Steps:

Enter the initial volume (\( V_1 \)) in mm³, cm³, in³, L, mL, ft³, yd³, or m³ (default is 2 L, step size 0.00001).
Enter the initial temperature (\( T_1 \)) in K, °C, or °F (default is 35 °C, step size 0.01).
Select whether to calculate the final volume (\( V_2 \)) or final temperature (\( T_2 \)).
If calculating \( V_2 \), enter the final temperature (\( T_2 \)) in K, °C, or °F (default is 15 °C, step size 0.01).
If calculating \( T_2 \), enter the final volume (\( V_2 \)) in mm³, cm³, in³, L, mL, ft³, yd³, or m³ (default is 1.8702 L, step size 0.00001).
Convert initial volume to m³ and temperatures to Kelvin.
Calculate the final parameter using the appropriate Charles' Law formula.
Convert the result back to the selected unit and display it, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.

3. Importance of Charles' Law Calculation

Calculating using Charles' Law is crucial for:

Gas Behavior Analysis: It helps predict how gases respond to temperature changes, such as in hot air balloons, tire pressure variations, and industrial gas storage.
Engineering Systems: Charles' Law is used in designing systems like HVAC units, engines, and refrigeration systems where gas volume changes with temperature.
Scientific Research: It aids in studying thermodynamic properties of gases under controlled conditions.

4. Using the Calculator

Examples:

Example 1: Calculate the final volume of a gas with an initial volume of 2 L at 35 °C when cooled to 15 °C:
- Enter Initial Volume = 2 L, convert to m³: \( 2 \times 0.001 = 0.002 \, \text{m}^3 \).
- Enter Initial Temperature = 35 °C, convert to K: \( 35 + 273.15 = 308.15 \, \text{K} \).
- Enter Final Temperature = 15 °C, convert to K: \( 15 + 273.15 = 288.15 \, \text{K} \).
- Final Volume: \( V_2 = V_1 \cdot \frac{T_2}{T_1} = 0.002 \cdot \frac{288.15}{308.15} = 0.0018702 \, \text{m}^3 \).
- Convert to L: \( 0.0018702 \times 1000 = 1.8702 \).
- Result: \( V_2 = 1.8702 \, \text{L} \).
Example 2: Calculate the final temperature of a gas with an initial volume of 0.03 ft³ at 22 °C when the volume expands to 0.062 ft³:
- Enter Initial Volume = 0.03 ft³, convert to m³: \( 0.03 \times 0.0283168 = 0.000849504 \, \text{m}^3 \).
- Enter Initial Temperature = 22 °C, convert to K: \( 22 + 273.15 = 295.15 \, \text{K} \).
- Enter Final Volume = 0.062 ft³, convert to m³: \( 0.062 \times 0.0283168 = 0.0017556416 \, \text{m}^3 \).
- Final Temperature: \( T_2 = T_1 \cdot \frac{V_2}{V_1} = 295.15 \cdot \frac{0.0017556416}{0.000849504} \approx 609.7 \, \text{K} \).
- Convert to °C: \( 609.7 - 273.15 = 336.55 \).
- Result: \( T_2 = 336.5500 \, \text{°C} \).

5. Frequently Asked Questions (FAQ)

Q: What does Charles' Law describe?
A: Charles' Law describes the direct relationship between the volume and temperature of a gas at constant pressure. When the temperature increases, the volume increases proportionally, and vice versa, as long as the pressure remains constant.

Q: Why must temperatures be in Kelvin?
A: Charles' Law requires absolute temperatures (Kelvin) because it involves temperature ratios, and Kelvin ensures positive values with a true zero point, avoiding negative values that would occur with Celsius or Fahrenheit.

Q: What are some real-world applications of Charles' Law?
A: Charles' Law applies to hot air balloons (where heating air increases volume to lift the balloon), vehicle tires (where temperature changes affect tire pressure), and baking (where dough rises as gases expand with heat).