Capacitors in Series Calculator

Number of Capacitors:

1. What is Capacitors in Series Calculator?

Definition: This calculator computes the equivalent capacitance (\( C_{\text{eq}} \)) of multiple capacitors connected in series.

Purpose: It is used in electronics to determine the total capacitance in a series circuit, which is essential for designing filters, timing circuits, and other applications involving capacitors.

2. How Does the Calculator Work?

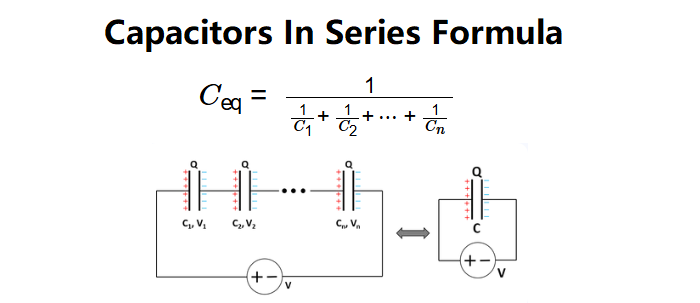
The calculator uses the formula for capacitors in series:

\( \frac{1}{C_{\text{eq}}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n} \)
\( C_{\text{eq}} = \frac{1}{\frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n}} \)

Where:

\( C_{\text{eq}} \): Equivalent capacitance (F)
\( C_1, C_2, \ldots, C_n \): Capacitance of each capacitor (F)

Steps:

Select the number of capacitors.
Enter the capacitance values for each capacitor with their units.
Convert all inputs to farads (F).
Calculate the sum of the inverses of the capacitances.
Compute the equivalent capacitance by taking the inverse of the sum.
Convert the result to the selected output unit.
Display the result with 4 decimal places.

3. Importance of Capacitors in Series Calculation

Calculating the equivalent capacitance of capacitors in series is crucial for:

Circuit Design: Determining the total capacitance in series circuits used in filters, timing circuits, or voltage dividers.
Component Selection: Choosing appropriate capacitors to achieve the desired total capacitance.
Voltage Distribution: Understanding how voltage is distributed across capacitors in series, as the total voltage is the sum of the voltages across each capacitor.

4. Using the Calculator

Example 1: Calculate the equivalent capacitance of four capacitors in series with \( C_1 = 2 \, \text{mF} \), \( C_2 = 5 \, \mu\text{F} \), \( C_3 = 6 \, \mu\text{F} \), and \( C_4 = 200 \, \text{nF} \):

Capacitance Values:
\( C_1 = 2 \, \text{mF} = 2 \times 10^{-3} \, \text{F} \)
\( C_2 = 5 \, \mu\text{F} = 5 \times 10^{-6} \, \text{F} \)
\( C_3 = 6 \, \mu\text{F} = 6 \times 10^{-6} \, \text{F} \)
\( C_4 = 200 \, \text{nF} = 200 \times 10^{-9} = 2 \times 10^{-7} \, \text{F} \)
Sum of inverses: \( \frac{1}{C_{\text{eq}}} = \frac{1}{2 \times 10^{-3}} + \frac{1}{5 \times 10^{-6}} + \frac{1}{6 \times 10^{-6}} + \frac{1}{2 \times 10^{-7}} \)
\( \frac{1}{C_{\text{eq}}} = 500 + 200000 + 166666.67 + 5000000 = 5367166.67 \, \text{F}^{-1} \)
Equivalent capacitance: \( C_{\text{eq}} = \frac{1}{5367166.67} \approx 1.863 \times 10^{-7} \, \text{F} = 0.1863 \, \mu\text{F} \)
Result: \( C_{\text{eq}} = 0.1863 \, \mu\text{F} \)

Example 2: Calculate the equivalent capacitance of two capacitors in series with \( C_1 = 10 \, \mu\text{F} \) and \( C_2 = 20 \, \mu\text{F} \):

Capacitance Values:
\( C_1 = 10 \, \mu\text{F} = 10 \times 10^{-6} \, \text{F} \)
\( C_2 = 20 \, \mu\text{F} = 20 \times 10^{-6} \, \text{F} \)
Sum of inverses: \( \frac{1}{C_{\text{eq}}} = \frac{1}{10 \times 10^{-6}} + \frac{1}{20 \times 10^{-6}} \)
\( \frac{1}{C_{\text{eq}}} = 100000 + 50000 = 150000 \, \text{F}^{-1} \)
Equivalent capacitance: \( C_{\text{eq}} = \frac{1}{150000} \approx 6.6667 \times 10^{-6} \, \text{F} = 6.6667 \, \mu\text{F} \)
Result: \( C_{\text{eq}} = 6.6667 \, \mu\text{F} \)

5. Frequently Asked Questions (FAQ)

Q: Why is the equivalent capacitance in series less than the smallest individual capacitance?
A: In a series connection, the inverse of the equivalent capacitance is the sum of the inverses of the individual capacitances, which results in a smaller total capacitance. This reflects the fact that the effective charge storage capacity is reduced.

Q: How does voltage distribute across capacitors in series?
A: The total voltage across the series combination is the sum of the voltages across each capacitor. The voltage across each capacitor is inversely proportional to its capacitance: \( V_i = \frac{Q}{C_i} \), where \( Q \) is the same for all capacitors in series.

Q: Can I use this calculator for capacitors in parallel?
A: No, this calculator is specifically for capacitors in series. For capacitors in parallel, the equivalent capacitance is the sum of the individual capacitances: \( C_{\text{eq}} = C_1 + C_2 + \cdots + C_n \).