Capacitors in Parallel Calculator

Number of Capacitors:

1. What is Capacitors in Parallel Calculator?

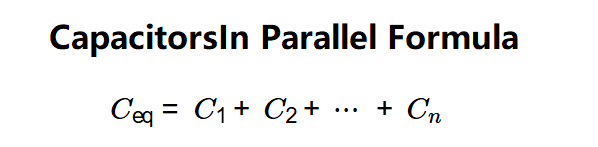
Definition: This calculator computes the equivalent capacitance (\( C_{\text{eq}} \)) of multiple capacitors connected in parallel.

Purpose: It is used in electronics to determine the total capacitance in a parallel circuit, which is essential for designing circuits requiring higher capacitance, such as power supplies, filters, and energy storage systems.

2. How Does the Calculator Work?

The calculator uses the formula for capacitors in parallel:

\( C_{\text{eq}} = C_1 + C_2 + \cdots + C_n \)

Where:

\( C_{\text{eq}} \): Equivalent capacitance (F)
\( C_1, C_2, \ldots, C_n \): Capacitance of each capacitor (F)

Steps:

Select the number of capacitors.
Enter the capacitance values for each capacitor with their units.
Convert all inputs to farads (F).
Calculate the sum of the capacitances.
Convert the result to the selected output unit.
Display the result with 4 decimal places.

3. Importance of Capacitors in Parallel Calculation

Calculating the equivalent capacitance of capacitors in parallel is crucial for:

Circuit Design: Achieving higher capacitance for applications like smoothing power supply outputs or tuning circuits.
Component Selection: Selecting capacitors to meet the required total capacitance.
Energy Storage: Increasing the charge storage capacity, as parallel capacitors store more charge at the same voltage.

4. Using the Calculator

Example 1: Calculate the equivalent capacitance of four capacitors in parallel with \( C_1 = 2 \, \text{mF} \), \( C_2 = 5 \, \mu\text{F} \), \( C_3 = 6 \, \mu\text{F} \), and \( C_4 = 200 \, \text{nF} \):

Capacitance Values:
\( C_1 = 2 \, \text{mF} = 2 \times 10^{-3} \, \text{F} \)
\( C_2 = 5 \, \mu\text{F} = 5 \times 10^{-6} \, \text{F} \)
\( C_3 = 6 \, \mu\text{F} = 6 \times 10^{-6} \, \text{F} \)
\( C_4 = 200 \, \text{nF} = 200 \times 10^{-9} = 2 \times 10^{-7} \, \text{F} \)
Sum of capacitances: \( C_{\text{eq}} = 2 \times 10^{-3} + 5 \times 10^{-6} + 6 \times 10^{-6} + 2 \times 10^{-7} \)
\( C_{\text{eq}} = 0.002 + 0.000005 + 0.000006 + 0.0000002 = 0.0020112 \, \text{F} \)
Convert to µF: \( 0.0020112 \, \text{F} = 2011.2 \, \mu\text{F} \)
Result: \( C_{\text{eq}} = 2011.2000 \, \mu\text{F} \)

Example 2: Calculate the equivalent capacitance of two capacitors in parallel with \( C_1 = 10 \, \mu\text{F} \) and \( C_2 = 20 \, \mu\text{F} \):

Capacitance Values:
\( C_1 = 10 \, \mu\text{F} = 10 \times 10^{-6} \, \text{F} \)
\( C_2 = 20 \, \mu\text{F} = 20 \times 10^{-6} \, \text{F} \)
Sum of capacitances: \( C_{\text{eq}} = 10 \times 10^{-6} + 20 \times 10^{-6} \)
\( C_{\text{eq}} = 30 \times 10^{-6} \, \text{F} = 30 \, \mu\text{F} \)
Result: \( C_{\text{eq}} = 30.0000 \, \mu\text{F} \)

5. Frequently Asked Questions (FAQ)

Q: Why is the equivalent capacitance in parallel greater than any individual capacitance?
A: In parallel, the effective plate area increases because the capacitors share the same voltage, allowing more charge to be stored, resulting in a higher total capacitance.

Q: How does charge distribute across capacitors in parallel?
A: The charge on each capacitor is proportional to its capacitance: \( Q_i = C_i \cdot V \), where \( V \) is the common voltage across all capacitors. The total charge is the sum of individual charges.

Q: Can I use this calculator for capacitors in series?
A: No, this calculator is specifically for capacitors in parallel. For capacitors in series, the equivalent capacitance is calculated using \( \frac{1}{C_{\text{eq}}} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots + \frac{1}{C_n} \).