Capacitor Energy Calculator

Calculation Mode:

Capacitance (

C

Voltage (

V

1. What is Capacitor Energy Calculator?

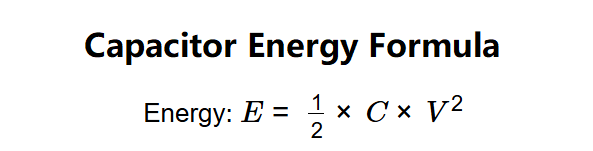
Definition: This calculator computes the energy ( $E$ ) stored in a capacitor based on its capacitance ( $C$ ), voltage ( $V$ ), or charge ( $Q$ ).

Purpose: It is used in electronics to determine the energy storage capacity of capacitors, which is essential for designing power supplies, energy storage systems, and circuits involving capacitors.

2. How Does the Calculator Work?

The calculator supports three modes:

Mode 1: Using Capacitance and Voltage ( $C$ and $V$ )

Energy: $E = \frac{1}{2} \times C \times V^{2}$

Mode 2: Using Charge and Capacitance ( $Q$ and $C$ )

Energy: $E = \frac{1}{2} \times \frac{Q^{2}}{C}$

Mode 3: Using Charge and Voltage ( $Q$ and $V$ )

Energy: $E = \frac{1}{2} \times Q \times V$

Where:

$E$ : Energy stored in the capacitor (J)
$C$ : Capacitance (F)
$V$ : Voltage across the capacitor (V)
$Q$ : Charge on the capacitor (C)

Steps:

Select the calculation mode.
Enter the required parameters ( $C$ and $V$ , $Q$ and $C$ , or $Q$ and $V$ ) with their units.
Convert all inputs to base units (F, V, C).
Calculate the energy using the appropriate formula.
Convert the result to the selected output unit.
Display the result with 4 decimal places.

3. Importance of Capacitor Energy Calculation

Calculating the energy stored in a capacitor is crucial for:

Energy Storage Systems: Determining how much energy a capacitor can store for applications like power backup or pulse circuits.
Circuit Design: Ensuring capacitors are appropriately sized for energy requirements in filters, timing circuits, or oscillators.
Safety: Understanding the energy stored to prevent overvoltage or discharge hazards in high-energy capacitors.

4. Using the Calculator

Example 1 (Mode 1: Capacitance and Voltage): A capacitor with a capacitance of 100 µF and a voltage of 10 V:

Capacitance ( $C$ ): 100 µF = $100 \times 10^{- 6}$ F = $10^{- 4}$ F
Voltage ( $V$ ): 10 V
Energy ( $E$ ): $\frac{1}{2} \times 10^{- 4} \times 10^{2} = \frac{1}{2} \times 10^{- 4} \times 100 = 0.005$ J = 5 mJ
Result: $E = 0.0050$ J (or 5.0000 mJ)

Example 2 (Mode 2: Charge and Capacitance): A capacitor with a charge of 0.001 C and capacitance of 100 µF:

Charge ( $Q$ ): 0.001 C
Capacitance ( $C$ ): 100 µF = $10^{- 4}$ F
Energy ( $E$ ): $Extra close brace or missing open brace$ J = 5 mJ
Result: $E = 0.0050$ J (or 5.0000 mJ)

Example 3 (Mode 3: Charge and Voltage): A capacitor with a charge of 0.001 C and a voltage of 10 V:

Charge ( $Q$ ): 0.001 C
Voltage ( $V$ ): 10 V
Energy ( $E$ ): $\frac{1}{2} \times 0.001 \times 10 = 0.005$ J = 5 mJ
Result: $E = 0.0050$ J (or 5.0000 mJ)

5. Frequently Asked Questions (FAQ)

Q: Why is the energy formula for a capacitor $E = \frac{1}{2} \times C \times V^{2}$ ?
A: The energy stored in a capacitor is the work done to charge it. As the voltage increases linearly with charge ( $V = Q / C$ ), the average voltage during charging is $V / 2$ , so the work done is $E = Q \times (V / 2)$ , which simplifies to $\frac{1}{2} \times C \times V^{2}$ .

Q: Can a capacitor store energy indefinitely?
A: No, capacitors can lose energy over time due to leakage currents or dielectric losses, especially in non-ideal capacitors.

Q: How does the energy change if the voltage doubles?
A: Since $E \propto V^{2}$ , doubling the voltage quadruples the energy stored in the capacitor.