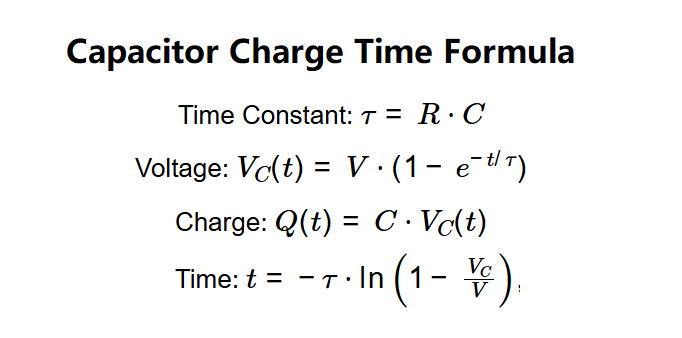Capacitor Charge Time Calculator

Calculation Mode:

Supply Voltage (\( V \)):

Resistance (\( R \)):

Capacitance (\( C \)):

Time (\( t \)):

Time Constant (\( \tau \)):

Capacitor Voltage (\( V_C \)):

Charge (\( Q \)):

1. What is Capacitor Charge Time Calculator?

Definition: This calculator computes the charging behavior of a capacitor in an RC circuit, including the time constant, voltage across the capacitor, charge, and the time to reach a specific charging percentage.

Purpose: It is used in electronics to analyze and design RC circuits, such as in timing circuits, filters, and power supplies, ensuring proper charging characteristics.

2. How Does the Calculator Work?

The calculator supports two modes:

Mode 1: Calculate Voltage and Charge at Time \( t \)

Time Constant: \( \tau = R \cdot C \)
Voltage: \( V_C(t) = V \cdot (1 - e^{-t / \tau}) \)
Charge: \( Q(t) = C \cdot V_C(t) \)

Mode 2: Calculate Time to Reach Charged Percentage

Time Constant: \( \tau = R \cdot C \)
Time: \( t = -\tau \cdot \ln\left(1 - \frac{V_C}{V}\right) \), where \( \frac{V_C}{V} \) is the charged percentage

Where:

\( \tau \): Time constant (s)
\( R \): Resistance (Ω)
\( C \): Capacitance (F)
\( V_C(t) \): Voltage across the capacitor at time \( t \) (V)
\( V \): Supply voltage (V)
\( t \): Time (s)
\( Q(t) \): Charge on the capacitor at time \( t \) (C)

Steps:

Select the calculation mode.
Enter the supply voltage (\( V \)), resistance (\( R \)), and capacitance (\( C \)) with their units.
Depending on the mode, enter either the time (\( t \)) or select the desired charged percentage (\( V_C / V \)).
Convert all inputs to base units (V, Ω, F, s).
Calculate the time constant and the requested parameters using the formulas.
Convert the results to the selected output units.
Display the results with 4 decimal places.

3. Importance of Capacitor Charge Time Calculation

Calculating capacitor charging parameters is crucial for:

Electronics Design: Ensuring proper timing in RC circuits used in filters, oscillators, and timing applications.
Performance: Determining how quickly a capacitor charges to a desired percentage of the supply voltage.
Component Selection: Choosing appropriate resistors and capacitors to achieve the desired time constant.

4. Using the Calculator

Example 1 (Mode 1: Voltage and Charge at Time \( t \)): A capacitor in an RC circuit with a supply voltage of 10 V, resistance of 1 kΩ, capacitance of 1 µF, and time of 1 ms:

Supply Voltage (\( V \)): 10 V
Resistance (\( R \)): 1 kΩ = 1000 Ω
Capacitance (\( C \)): 1 µF = \( 1 \times 10^{-6} \) F
Time (\( t \)): 1 ms = 0.001 s
Time Constant (\( \tau \)): \( R \cdot C = 1000 \times 10^{-6} = 0.001 \) s
Voltage (\( V_C \)): \( 10 \cdot (1 - e^{-0.001 / 0.001}) \approx 10 \cdot (1 - e^{-1}) \approx 6.3212 \) V
Charge (\( Q \)): \( C \cdot V_C = 10^{-6} \times 6.3212 \approx 6.3212 \times 10^{-6} \) C = 6.3212 µC
Result: \( \tau = 0.0010 \) s (or 1.0000 ms), \( V_C = 6.3212 \) V, \( Q = 6.3212 \) µC

Example 2 (Mode 2: Time to Reach Charged Percentage): A capacitor in an RC circuit with a supply voltage of 10 V, resistance of 1 kΩ, capacitance of 1 µF, and desired charged percentage of 63.2% (1τ):

Supply Voltage (\( V \)): 10 V
Resistance (\( R \)): 1 kΩ = 1000 Ω
Capacitance (\( C \)): 1 µF = \( 1 \times 10^{-6} \) F
Charged Percentage: 63.2%
Desired Voltage (\( V_C \)): \( 10 \times \frac{63.2}{100} = 6.32 \) V
Time Constant (\( \tau \)): \( R \cdot C = 1000 \times 10^{-6} = 0.001 \) s
Time (\( t \)): \( -0.001 \cdot \ln\left(1 - \frac{6.32}{10}\right) = -0.001 \cdot \ln(0.368) \approx 0.001 \) s = 1 ms
Result: \( \tau = 0.0010 \) s (or 1.0000 ms), \( t = 1.0000 \) ms

5. Frequently Asked Questions (FAQ)

Q: What is the time constant of an RC circuit?
A: The time constant (\( \tau \)) is the product of resistance (\( R \)) and capacitance (\( C \)), representing the time it takes for the capacitor to charge to about 63.2% of the supply voltage.

Q: Why does the capacitor voltage never reach the supply voltage?
A: The charging process follows an exponential curve, approaching the supply voltage asymptotically but never fully reaching it in finite time.

Q: How long does it take for a capacitor to fully charge?
A: In practice, a capacitor is considered fully charged after about 5 time constants (\( 5\tau \)), when it reaches approximately 99.3% of the supply voltage.