Bulk Modulus Calculator

Pressure Applied (\( \Delta P \)):

Change in Volume (\( \Delta V \)):

Initial Volume (\( V_0 \)):

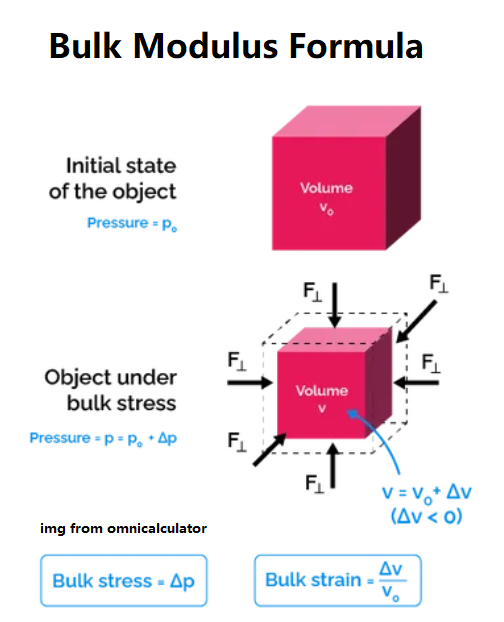
1. What is Bulk Modulus Calculator?

Definition: This calculator computes the bulk modulus (\( B \)), a measure of a material's resistance to uniform compression, and the bulk strain (\( \Delta V / V_0 \)), the fractional change in volume under pressure.

Purpose: It is used in material science and engineering to understand how materials respond to pressure, aiding in the design of materials and structures under compressive forces.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ \text{Bulk Strain} = \frac{\Delta V}{V_0} \] \[ B = -\frac{\Delta P}{\left(\frac{\Delta V}{V_0}\right)} \] Where:

\( \text{Bulk Strain} \): Fractional change in volume (dimensionless)
\( B \): Bulk modulus (Pa, kPa, MPa, GPa, psi)
\( \Delta P \): Pressure applied (Pa, kPa, MPa, GPa, psi)
\( \Delta V \): Change in volume (m³, cm³, mm³, in³, ft³)
\( V_0 \): Initial volume (m³, cm³, mm³, in³, ft³)

Unit Conversions:

Pressure (\( \Delta P \), \( B \)):
- 1 Pa = 1 Pa
- 1 kPa = 1000 Pa
- 1 MPa = 1000000 Pa
- 1 GPa = 1000000000 Pa
- 1 psi = 6894.76 Pa
Volume (\( \Delta V \), \( V_0 \)):
- 1 m³ = 1 m³
- 1 cm³ = 1e-6 m³
- 1 mm³ = 1e-9 m³
- 1 in³ = 1.6387e-5 m³
- 1 ft³ = 0.0283168 m³
Bulk Strain (\( \Delta V / V_0 \)): Dimensionless

Steps:

Enter the pressure applied (\( \Delta P \)), change in volume (\( \Delta V \)), and initial volume (\( V_0 \)) with their respective units.
Convert the pressure to Pa and the volumes to m³.
Calculate the bulk strain as \( \frac{\Delta V}{V_0} \).
Calculate the bulk modulus as \( B = -\frac{\Delta P}{\left(\frac{\Delta V}{V_0}\right)} \).
Convert the bulk modulus to the selected unit.
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Bulk Modulus Calculation

Calculating the bulk modulus is crucial for:

Material Science: Understanding how materials resist compression under pressure.
Engineering Design: Designing materials and structures that can withstand compressive forces.
Geophysics: Analyzing the behavior of materials under high pressure, such as in the Earth's interior.

4. Using the Calculator

Examples:

Example 1: For \( \Delta P = 12 \, \text{Pa} \), \( \Delta V = -0.4 \, \text{m}^3 \), \( V_0 = 0.2 \, \text{m}^3 \), bulk modulus in Pa:
- Bulk Strain: \( \frac{\Delta V}{V_0} = \frac{-0.4}{0.2} = -2.0000 \)
- Bulk Modulus: \( B = -\frac{12}{-2} = 6.0000 \, \text{Pa} \)
Example 2: For \( \Delta P = 1 \, \text{MPa} \), \( \Delta V = -0.5 \, \text{cm}^3 \), \( V_0 = 2 \, \text{cm}^3 \), bulk modulus in MPa:
- Convert: \( \Delta P = 1 \times 1000000 = 1000000 \, \text{Pa} \), \( \Delta V = -0.5 \times 1e-6 = -5e-7 \, \text{m}^3 \), \( V_0 = 2 \times 1e-6 = 2e-6 \, \text{m}^3 \)
- Bulk Strain: \( \frac{\Delta V}{V_0} = \frac{-5e-7}{2e-6} = -0.2500 \)
- Bulk Modulus: \( B = -\frac{1000000}{-0.25} = 4000000 \, \text{Pa} \)
- Convert to MPa: \( 4000000 / 1000000 = 4.0000 \, \text{MPa} \)

5. Frequently Asked Questions (FAQ)

Q: What is bulk modulus?
A: Bulk modulus (\( B \)) is a measure of a material's resistance to uniform compression, defined as the negative ratio of pressure applied to the fractional change in volume.

Q: What is bulk strain?
A: Bulk strain (\( \Delta V / V_0 \)) is the fractional or percentual change in volume caused by pressure stress. It is negative for compression.

Q: How is bulk modulus used in real life?
A: It is used in material science to study compressibility, in engineering to design pressure-resistant structures, and in geophysics to understand material behavior under high pressure.