Bridged Tee Attenuator Calculator

Resistor Value (\( R1 \)):

Resistor Value (\( R2 \)):

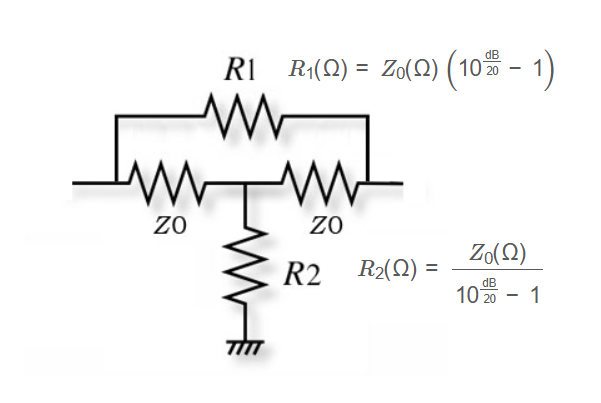
1. What is a Bridged-Tee Attenuator Calculator?

Definition: This calculator determines the resistor values \( R1 \) and \( R2 \) for a Bridged-Tee attenuator circuit based on the desired attenuation and the characteristic impedance \( Z_0 \).

Purpose: It helps engineers and RF designers select appropriate resistor values for attenuator circuits used in RF and microwave applications to control signal levels while maintaining impedance matching.

2. How Does the Calculator Work?

The calculator uses the following formulas to compute the resistor values:

Resistor \( R1 \): \[ R_1(\Omega) = Z_0(\Omega) \left( 10^{\frac{\text{dB}}{20}} - 1 \right) \]

Resistor \( R2 \): \[ R_2(\Omega) = \frac{Z_0(\Omega)}{10^{\frac{\text{dB}}{20}} - 1} \]

Where:

\( R1, R2 \): Resistor values in ohms for the Bridged-Tee attenuator circuit
\( Z_0 \): Characteristic impedance in ohms (e.g., 50 ohms for typical RF systems)
dB: Attenuation in decibels

Unit Conversions:

Attenuation:
1 Np = 8.686 dB
Impedance and Resistors (\( R1, R2 \)):
1 kΩ = 1000 Ω
1 mΩ = 0.001 Ω

Steps:

Enter the desired attenuation and select the unit (dB or Np).
Enter the characteristic impedance \( Z_0 \) and select the unit (ohms, kΩ, or mΩ).
Click "Calculate" to compute \( R1 \) and \( R2 \).
The results are initially displayed in ohms.
Select a different unit for each resistor (ohms, kΩ, or mΩ) from the dropdowns after each result to convert the displayed values.

3. Importance of Bridged-Tee Attenuator Calculation

Calculating resistor values for a Bridged-Tee attenuator is essential for:

Signal Control: Attenuators reduce signal amplitude without distorting the waveform, critical in RF systems.
Impedance Matching: Ensures minimal signal reflection in high-frequency circuits.
Design Efficiency: Helps engineers select standard resistor values for practical implementation.

4. Using the Calculator

Examples:

Example 1: Attenuation = 10 dB, \( Z_0 \) = 50 ohms, Results in ohms
- Term: \( 10^{\frac{10}{20}} - 1 = 10^{0.5} - 1 \approx 3.162 - 1 = 2.162 \)
- \( R1 = 50 \times 2.162 \approx 108.10 \, \text{ohms} \)
- \( R2 = \frac{50}{2.162} \approx 23.13 \, \text{ohms} \)
Example 2: Attenuation = 0.691 Np, \( Z_0 \) = 0.075 kΩ, Results in mΩ
- Convert: Attenuation = \( 0.691 \times 8.686 \approx 6 \, \text{dB} \), \( Z_0 = 0.075 \times 1000 = 75 \, \text{ohms} \)
- Term: \( 10^{\frac{6}{20}} - 1 = 10^{0.3} - 1 \approx 1.995 - 1 = 0.995 \)
- \( R1 = 75 \times 0.995 \approx 74.63 \, \text{ohms} \)
- \( R2 = \frac{75}{0.995} \approx 75.38 \, \text{ohms} \)
- Results in mΩ: \( R1 = 74630 \, \text{mΩ} \), \( R2 = 75380 \, \text{mΩ} \)
Example 3: Attenuation = 3 dB, \( Z_0 \) = 60000 mΩ, Results in kΩ
- Convert: \( Z_0 = 60000 \times 0.001 = 60 \, \text{ohms} \)
- Term: \( 10^{\frac{3}{20}} - 1 = 10^{0.15} - 1 \approx 1.4125 - 1 = 0.4125 \)
- \( R1 = 60 \times 0.4125 \approx 24.75 \, \text{ohms} \)
- \( R2 = \frac{60}{0.4125} \approx 145.45 \, \text{ohms} \)
- Results in kΩ: \( R1 = 0.0248 \, \text{kΩ} \), \( R2 = 0.1455 \, \text{kΩ} \)

5. Frequently Asked Questions (FAQ)

Q: What is a Bridged-Tee attenuator?
A: A Bridged-Tee attenuator is a circuit configuration used in RF systems to reduce signal power while maintaining impedance matching, consisting of resistors arranged in a bridged-T topology.

Q: Can this calculator be used for other attenuator types?
A: No, this calculator is specific to Bridged-Tee attenuators with the given formulas. Other configurations (e.g., Pi, T, or balanced attenuators) require different formulas.

Q: What if the calculated resistor values are not standard?
A: In practice, select the closest standard resistor value (e.g., E12 or E24 series) or use a combination of resistors to approximate the calculated values.