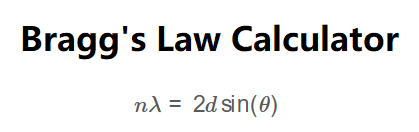Bragg's Law Calculator (Incidence Angle)

Order (\( n \)):

Wavelength (\( \lambda \)):

Interplanar Distance (\( d \)):

1. What is Bragg's Law Calculator (Incidence Angle)?

Definition: This calculator computes the incidence angle (\( \theta \)) of X-rays using Bragg's Law, which relates the wavelength of X-rays, the interplanar distance in a crystal, and the diffraction order.

Purpose: It is used in crystallography to determine the angle at which X-rays must strike a crystal to produce a diffraction pattern of a specific order.

2. How Does the Calculator Work?

The calculator uses Bragg's Law:

Formula: \[ n\lambda = 2d \sin(\theta) \] Rearranged to solve for \( \theta \): \[ \theta = \arcsin\left(\frac{n\lambda}{2d}\right) \] Where:

\( \theta \): Incidence angle of the X-ray (rad, deg)
\( n \): Diffraction order (positive integer)
\( \lambda \): Wavelength of the X-ray (m, mm, μm, nm, pm, Å)
\( d \): Interplanar distance (m, mm, μm, nm, pm, Å)

Unit Conversions:

Wavelength (\( \lambda \)) and Interplanar Distance (\( d \)): m, mm (1 mm = \( 10^{-3} \) m), μm (1 μm = \( 10^{-6} \) m), nm (1 nm = \( 10^{-9} \) m), pm (1 pm = \( 10^{-12} \) m), Å (1 Å = \( 10^{-10} \) m)
Angle (\( \theta \)): rad, deg (1 deg = \( \frac{\pi}{180} \) rad)

Steps:

Enter the diffraction order (\( n \)), wavelength (\( \lambda \)), and interplanar distance (\( d \)), and select their units.
Convert all inputs to base units (m for \( \lambda \) and \( d \)).
Calculate \( \sin(\theta) \) using \( \sin(\theta) = \frac{n\lambda}{2d} \).
Compute \( \theta = \arcsin\left(\frac{n\lambda}{2d}\right) \) in radians.
Convert the result to the selected unit (rad or deg).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Incidence Angle Calculation

Calculating the incidence angle using Bragg's Law is crucial for:

Crystallography: Setting the correct angle for X-ray diffraction experiments to observe specific diffraction patterns.
Material Science: Analyzing the atomic structure of materials by ensuring proper diffraction conditions.
Education: Understanding the relationship between wave interference and crystal geometry in physics.

4. Using the Calculator

Examples:

Example 1: For \( n = 1 \), \( \lambda = 154 \, \text{pm} \), \( d = 314 \, \text{pm} \), angle in degrees:
- Convert: \( \lambda = 154 \times 10^{-12} \, \text{m} \), \( d = 314 \times 10^{-12} \, \text{m} \)
- \( \sin(\theta) = \frac{1 \times 154 \times 10^{-12}}{2 \times 314 \times 10^{-12}} = 0.2452 \)
- \( \theta = \arcsin(0.2452) \approx 0.2474 \, \text{rad} \)
- Convert to degrees: \( \theta = 0.2474 \times \frac{180}{\pi} \approx 14.1735^\circ \)
Example 2: For \( n = 2 \), \( \lambda = 0.154 \, \text{nm} \), \( d = 0.282 \, \text{nm} \), angle in radians:
- Convert: \( \lambda = 0.154 \times 10^{-9} \, \text{m} \), \( d = 0.282 \times 10^{-9} \, \text{m} \)
- \( \sin(\theta) = \frac{2 \times 0.154 \times 10^{-9}}{2 \times 0.282 \times 10^{-9}} = 0.5461 \)
- \( \theta = \arcsin(0.5461) \approx 0.5736 \, \text{rad} \)

5. Frequently Asked Questions (FAQ)

Q: What is the incidence angle in Bragg's Law?
A: The incidence angle (\( \theta \)) is the angle at which X-rays strike the crystal planes, measured relative to the plane's surface.

Q: Why must \( n\lambda / (2d) \) be between 0 and 1?
A: Since \( \sin(\theta) \) must be between 0 and 1 for \( \theta \) to be a real angle, \( \frac{n\lambda}{2d} \) must also be in this range.

Q: How do I measure the incidence angle experimentally?
A: In X-ray diffraction experiments, the angle is adjusted using a goniometer to find the position where constructive interference (diffraction peaks) occurs.