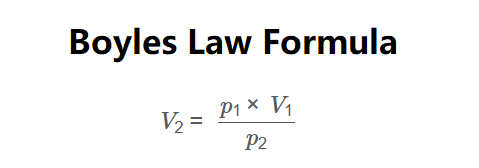1. What is the Boyle's Law Calculator?
Definition: This calculator uses Boyle's Law to compute the final volume (\( V_2 \)) of a gas at constant temperature, given the initial pressure (\( p_1 \)), initial volume (\( V_1 \)), and final pressure (\( p_2 \)). Boyle's Law states that for a fixed amount of gas at constant temperature, the product of pressure and volume is constant.
Purpose: It is used in physics and engineering to analyze the behavior of gases under changing pressure conditions, such as in gas storage, piston systems, and respiratory mechanics.
2. How Does the Calculator Work?
The calculator uses Boyle's Law:
Formula:
\[
p_1 \times V_1 = p_2 \times V_2 \implies V_2 = \frac{p_1 \times V_1}{p_2}
\]
where:
- \( p_1 \): Initial pressure (Pa, bar, atm, psi, kPa, mmHg)
- \( V_1 \): Initial volume (mm³, cm³, in³, L, mL, ft³, yd³, m³)
- \( p_2 \): Final pressure (Pa, bar, atm, psi, kPa, mmHg)
- \( V_2 \): Final volume (mm³, cm³, in³, L, mL, ft³, yd³, m³)
Unit Conversions:
- Pressure (\( p_1 \), \( p_2 \)):
- 1 Pa = 1 Pa
- 1 bar = 100000 Pa
- 1 atm = 101325 Pa
- 1 psi = 6894.76 Pa
- 1 kPa = 1000 Pa
- 1 mmHg = 133.322 Pa
- Volume (\( V_1 \), \( V_2 \)):
- 1 mm³ = \( 1 \times 10^{-9} \, \text{m}^3 \)
- 1 cm³ = \( 1 \times 10^{-6} \, \text{m}^3 \)
- 1 in³ = \( 1.63871 \times 10^{-5} \, \text{m}^3 \)
- 1 L = 0.001 m³
- 1 mL = \( 1 \times 10^{-6} \, \text{m}^3 \)
- 1 ft³ = 0.0283168 m³
- 1 yd³ = 0.764555 m³
- 1 m³ = 1 m³
Steps:
- Enter the initial pressure (\( p_1 \)) in Pa, bar, atm, psi, kPa, or mmHg (default is 1 atm, step size 0.00001).
- Enter the initial volume (\( V_1 \)) in mm³, cm³, in³, L, mL, ft³, yd³, or m³ (default is 1 L, step size 0.00001).
- Enter the final pressure (\( p_2 \)) in Pa, bar, atm, psi, kPa, or mmHg (default is 0.5 atm, step size 0.00001).
- Convert initial pressure to Pa, initial volume to m³, and final pressure to Pa.
- Calculate the final volume (\( V_2 \)) as \( V_2 = \frac{p_1 \times V_1}{p_2} \).
- Convert the calculated final volume to the selected unit (default is L) and display the result, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.
3. Importance of Boyle's Law Calculation
Calculating using Boyle's Law is crucial for:
- Gas Behavior Analysis: It helps predict how gases respond to changes in pressure, such as in gas storage, scuba diving, and balloon flight.
- Engineering Systems: Boyle's Law is used in designing systems like compressors, pneumatic devices, and engines where gases are compressed or expanded.
- Medical Applications: It applies to respiratory mechanics, such as understanding how air moves in and out of the lungs during breathing.
4. Using the Calculator
Examples:
- Example 1: Calculate the final volume with an initial pressure of 1 atm, initial volume of 1 L, and final pressure of 0.5 atm, in L:
- Enter Initial Pressure = 1 atm, convert to Pa: \( 1 \times 101325 = 101325 \, \text{Pa} \).
- Enter Initial Volume = 1 L, convert to m³: \( 1 \times 0.001 = 0.001 \, \text{m}^3 \).
- Enter Final Pressure = 0.5 atm, convert to Pa: \( 0.5 \times 101325 = 50662.5 \, \text{Pa} \).
- Final Volume: \( V_2 = \frac{p_1 \times V_1}{p_2} = \frac{101325 \times 0.001}{50662.5} = 0.002 \, \text{m}^3 \).
- Convert to L: \( 0.002 \times 1000 = 2 \).
- Result: \( V_2 = 2.0000 \, \text{L} \).
- Change output to mm³: \( 2 \, \text{L} = 2 \times 10^6 \, \text{mm}^3 = 2000000.0000 \, \text{mm}^3 \).
- Example 2: Calculate the final volume with an initial pressure of 2 bar, initial volume of 500 mm³, and final pressure of 1 bar, in mm³:
- Enter Initial Pressure = 2 bar, convert to Pa: \( 2 \times 100000 = 200000 \, \text{Pa} \).
- Enter Initial Volume = 500 mm³, convert to m³: \( 500 \times 10^{-9} = 5 \times 10^{-7} \, \text{m}^3 \).
- Enter Final Pressure = 1 bar, convert to Pa: \( 1 \times 100000 = 100000 \, \text{Pa} \).
- Final Volume: \( V_2 = \frac{p_1 \times V_1}{p_2} = \frac{200000 \times 5 \times 10^{-7}}{100000} = 1 \times 10^{-6} \, \text{m}^3 \).
- Convert to L: \( 1 \times 10^{-6} \times 1000 = 0.001 \, \text{L} \).
- Result (default unit L): \( V_2 = 0.0010 \, \text{L} \).
- Change output to mm³: \( 1 \times 10^{-6} \times 10^9 = 1000 \).
- Result: \( V_2 = 1000.0000 \, \text{mm}^3 \).
5. Frequently Asked Questions (FAQ)
Q: What does Boyle's Law describe?
A: Boyle's Law describes the inverse relationship between the pressure and volume of a gas at constant temperature. When the pressure of a gas increases, its volume decreases, and vice versa, as long as the temperature remains constant.
Q: Why is temperature constant in Boyle's Law?
A: Boyle's Law applies only when the temperature of the gas is held constant because temperature affects the kinetic energy of gas particles. If temperature changes, the relationship between pressure and volume is governed by the combined gas law, which includes temperature effects.
Q: What are some real-world applications of Boyle's Law?
A: Boyle's Law is applied in various fields, such as scuba diving (where tank pressure changes with depth), syringe operation in medicine (where volume changes affect pressure), and the design of pneumatic systems like air pumps and compressors.
 Home
Home
 Back
Back