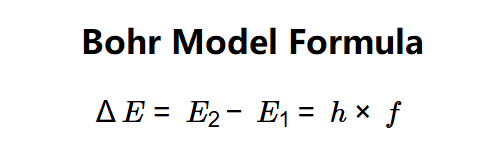Bohr Model Calculator

Initial Energy Level (\( E_2 \)):

Final Energy Level (\( E_1 \)):

Energy Difference (\( \Delta E \)):

Photon Frequency (\( f \)):

1. What is the Bohr Model Calculator?

Definition: This calculator uses the Bohr model equation to compute the energy difference (\( \Delta E \)) between two energy levels of an electron and the frequency (\( f \)) of the emitted or absorbed photon.

Purpose: It is used in quantum mechanics to predict the frequency of electromagnetic waves emitted or absorbed by an electron transitioning between energy levels in an atom, particularly for hydrogen in the Bohr model.

2. How Does the Calculator Work?

The calculator uses the following equation:

\( \Delta E = E_2 - E_1 = h \times f \)

Where:

\( E_2 \): Initial energy level of the electron (J, kJ, MJ, or eV);
\( E_1 \): Final energy level of the electron (J, kJ, MJ, or eV);
\( \Delta E \): Energy difference between the levels (J, kJ, MJ, or eV);
\( f \): Frequency of the emitted/absorbed photon (Hz, kHz, MHz, GHz, THz, or rpm);
\( h \): Planck's constant (\( 6.6261 \times 10^{-34} \, \text{J·s} \)).

Steps:

Enter the initial energy level (\( E_2 \)) with its unit.
Enter the final energy level (\( E_1 \)) with its unit.
Convert all inputs to Joules.
Calculate the energy difference: \( \Delta E = E_2 - E_1 \).
Calculate the frequency: \( f = \frac{|\Delta E|}{h} \).
Convert the energy difference and frequency to the selected output units and display both \( \Delta E \) and \( f \), formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Bohr Model Calculation

Calculating the energy difference and photon frequency in the Bohr model is crucial for:

Spectroscopy: Understanding the spectral lines of hydrogen and other elements.
Quantum Mechanics Education: Illustrating the quantized nature of electron energy levels in atoms.
Atomic Physics: Predicting the behavior of electrons in simple atomic systems.

4. Using the Calculator

Example 1: Calculate \( \Delta E \) and \( f \) for an electron transitioning between the following energy levels:

Initial Energy: \( E_2 = -3.4 \, \text{eV} \);
Final Energy: \( E_1 = -13.6 \, \text{eV} \);
Convert to Joules: \( E_2 = -3.4 \times 1.60218 \times 10^{-19} \approx -5.4474 \times 10^{-19} \, \text{J} \), \( E_1 = -13.6 \times 1.60218 \times 10^{-19} \approx -2.1789 \times 10^{-18} \, \text{J} \);
Energy Difference: \( \Delta E = -5.4474 \times 10^{-19} - (-2.1789 \times 10^{-18}) = 1.6342 \times 10^{-18} \, \text{J} \);
Frequency: \( f = \frac{1.6342 \times 10^{-18}}{6.6261 \times 10^{-34}} \approx 2.4665 \times 10^{15} \, \text{Hz} \);
Result: \( \Delta E = 10.2000 \, \text{eV} \), \( f = 2.4665 \times 10^{15} \, \text{Hz} \).

Example 2 (Different Units): Calculate \( \Delta E \) and \( f \) with the following properties:

Initial Energy: \( E_2 = -2.176 \times 10^{-18} \, \text{J} \);
Final Energy: \( E_1 = -5.44 \times 10^{-19} \, \text{J} \);
Energy Difference: \( \Delta E = -2.176 \times 10^{-18} - (-5.44 \times 10^{-19}) = -1.632 \times 10^{-18} \, \text{J} \);
Frequency: \( f = \frac{|-1.632 \times 10^{-18}|}{6.6261 \times 10^{-34}} \approx 2.4626 \times 10^{15} \, \text{Hz} \);
Result (in selected units, e.g., kJ and THz): \( \Delta E = -1.6320 \times 10^{-21} \, \text{kJ} \), \( f = 2462.6000 \, \text{THz} \).

5. Frequently Asked Questions (FAQ)

Q: What does a positive \( \Delta E \) mean?
A: A positive \( \Delta E \) indicates that the electron emits a photon as it transitions to a lower energy level (\( E_2 > E_1 \)).

Q: What does a negative \( \Delta E \) mean?
A: A negative \( \Delta E \) indicates that the electron absorbs a photon to transition to a higher energy level (\( E_2 < E_1 \)).

Q: Is this calculator applicable to atoms other than hydrogen?
A: The Bohr model is most accurate for hydrogen. For other atoms, more complex models like quantum mechanics are needed due to electron-electron interactions.