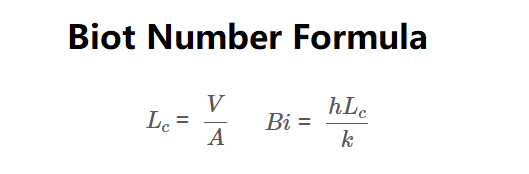1. What is the Biot Number Calculator?
Definition: This calculator computes the characteristic length (\( L_c \)) and the Biot number (\( Bi \)) for a material based on its surface area, volume, heat transfer coefficient, and thermal conductivity. The Biot number is a dimensionless quantity used to characterize heat transfer problems.
Purpose: It is used in heat transfer analysis to determine whether the temperature distribution within a solid can be considered uniform (low Biot number, \( Bi < 0.1 \)) or if significant temperature gradients exist (high Biot number, \( Bi > 0.1 \)), aiding in the design of thermal systems.
2. How Does the Calculator Work?
The calculator uses the following formulas:
Characteristic Length (\( L_c \)):
\[
L_c = \frac{V}{A}
\]
Biot Number (\( Bi \)):
\[
Bi = \frac{h L_c}{k}
\]
where:
- \( L_c \): Characteristic length (m, cm, ft, in)
- \( V \): Volume of the material (m³, cm³, ft³, in³)
- \( A \): Surface area of the material (m², cm², ft², in²)
- \( h \): Heat transfer coefficient at the material's surface (W/m²·K, W/cm²·K, Btu/hr·ft²·°F)
- \( k \): Thermal conductivity of the material (W/m·K, W/cm·K, Btu/hr·ft·°F)
- \( Bi \): Biot number (dimensionless)
Unit Conversions:
- Surface Area (\( A \)):
- 1 m² = 1 m²
- 1 cm² = 0.0001 m²
- 1 ft² = 0.092903 m²
- 1 in² = 0.00064516 m²
- Volume (\( V \)):
- 1 m³ = 1 m³
- 1 cm³ = 0.000001 m³
- 1 ft³ = 0.0283168 m³
- 1 in³ = 0.0000163871 m³
- Heat Transfer Coefficient (\( h \)):
- 1 W/m²·K = 1 W/m²·K
- 1 W/cm²·K = 10000 W/m²·K
- 1 Btu/hr·ft²·°F = 5.678263 W/m²·K
- Thermal Conductivity (\( k \)):
- 1 W/m·K = 1 W/m·K
- 1 W/cm·K = 100 W/m·K
- 1 Btu/hr·ft·°F = 1.730735 W/m·K
- Characteristic Length (\( L_c \)) for Output:
- 1 m = 1 m
- 1 m = 100 cm
- 1 m = 3.28084 ft
- 1 m = 39.3701 in
Steps:
- Enter the surface area in m², cm², ft², or in² (default is 1 m², step size 0.00001).
- Enter the volume in m³, cm³, ft³, or in³ (default is 0.1 m³, step size 0.00001).
- Enter the heat transfer coefficient in W/m²·K, W/cm²·K, or Btu/hr·ft²·°F (default is 50 W/m²·K, step size 0.00001).
- Enter the thermal conductivity in W/m·K, W/cm·K, or Btu/hr·ft·°F (default is 1 W/m·K, step size 0.00001).
- Convert surface area to m², volume to m³, heat transfer coefficient to W/m²·K, and thermal conductivity to W/m·K.
- Calculate the characteristic length (\( L_c \)) as \( V / A \).
- Calculate the Biot number (\( Bi \)) as \( h L_c / k \).
- Convert the characteristic length to the selected length unit and display both results, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.
3. Importance of Biot Number Calculation
Calculating the Biot number is crucial for:
- Heat Transfer Analysis: The Biot number determines whether the lumped capacitance method can be used (low \( Bi \), uniform temperature) or if internal temperature gradients must be considered (high \( Bi \)), guiding the choice of heat transfer models.
- Engineering Design: It helps engineers design systems like heat exchangers, cooling fins, and thermal insulation by understanding how heat penetrates a material.
- Material Selection: The Biot number informs material selection based on thermal conductivity and geometry, ensuring efficient heat transfer in applications like electronics cooling or building insulation.
4. Using the Calculator
Examples:
- Example 1: Calculate the characteristic length and Biot number with a surface area of 1 m², volume of 0.1 m³, heat transfer coefficient of 50 W/m²·K, and thermal conductivity of 1 W/m·K, with characteristic length in meters:
- Enter Surface Area = 1 m².
- Enter Volume = 0.1 m³.
- Enter Heat Transfer Coefficient = 50 W/m²·K.
- Enter Thermal Conductivity = 1 W/m·K.
- Characteristic Length: \( L_c = \frac{0.1}{1} = 0.1 \, \text{m} \).
- Biot Number: \( Bi = \frac{50 \times 0.1}{1} = 5 \).
- Result: \( L_c = 0.1000 \, \text{m}, Bi = 5.0000 \).
- Example 2: Calculate the characteristic length and Biot number with a surface area of 1000 cm², volume of 5000 cm³, heat transfer coefficient of 0.005 W/cm²·K, and thermal conductivity of 0.02 W/cm·K, with characteristic length in centimeters:
- Enter Surface Area = 1000 cm², convert to m²: \( 1000 \times 0.0001 = 0.1 \, \text{m}^2 \).
- Enter Volume = 5000 cm³, convert to m³: \( 5000 \times 0.000001 = 0.005 \, \text{m}^3 \).
- Enter Heat Transfer Coefficient = 0.005 W/cm²·K, convert to W/m²·K: \( 0.005 \times 10000 = 50 \, \text{W/m}^2\cdot\text{K} \).
- Enter Thermal Conductivity = 0.02 W/cm·K, convert to W/m·K: \( 0.02 \times 100 = 2 \, \text{W/m}\cdot\text{K} \).
- Characteristic Length: \( L_c = \frac{0.005}{0.1} = 0.05 \, \text{m} \), convert to cm: \( 0.05 \times 100 = 5 \).
- Biot Number: \( Bi = \frac{50 \times 0.05}{2} = 1.25 \).
- Result: \( L_c = 5.0000 \, \text{cm}, Bi = 1.2500 \).
5. Frequently Asked Questions (FAQ)
Q: What does the Biot number tell us?
A: The Biot number (\( Bi \)) compares the resistance to heat transfer inside a material (conduction) to the resistance at its surface (convection). A low \( Bi \) (less than 0.1) indicates that the material's temperature is relatively uniform, while a high \( Bi \) (greater than 0.1) suggests significant temperature gradients within the material.
Q: What is the characteristic length?
A: The characteristic length (\( L_c \)) is a geometric parameter defined as the ratio of the material's volume to its surface area (\( V / A \)). It represents the typical length scale over which heat conduction occurs within the material.
Q: Why are the heat transfer coefficient and thermal conductivity important?
A: The heat transfer coefficient (\( h \)) quantifies the rate of heat transfer at the material's surface due to convection, while the thermal conductivity (\( k \)) measures the material's ability to conduct heat internally. Together, they determine how heat flows into or out of the material, which is critical for the Biot number calculation.
 Home
Home
 Back
Back