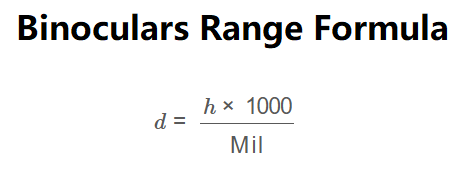Binoculars Range Calculator

Object Height (\( h \)):

Angular Height (\( \text{Mil} \)):

1. What is a Binoculars Range Calculator?

Definition: This calculator computes the distance (\( d \)) to an object using the binoculars range formula, which relies on the object's height and its angular height in milliradians.

Purpose: It is used in military and outdoor activities to estimate the distance to a target or object by observing its apparent size through binoculars with a reticle.

2. How Does the Calculator Work?

The calculator uses the binoculars range formula:

Distance: \[ d = \frac{h \times 1000}{\text{Mil}} \] Where:

\( d \): Distance to the object (mm, cm, m, km, in, ft, yd, mi)
\( h \): Object height (mm, cm, m, km, in, ft, yd, mi)
\( \text{Mil} \): Angular height in milliradians (mrad, rad, deg, arcmin, arcsec, μrad)

Unit Conversions:

Object Height (\( h \)) and Distance (\( d \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, km (1 km = 1000 m), in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m), mi (1 mi = 1609.344 m)
Angular Height (\( \text{Mil} \)): mrad, rad (1 rad = 1000 mrad), deg (1 deg = \( \frac{\pi}{180} \times 1000 \) mrad), arcmin (1 arcmin = \( \frac{\pi}{180 \times 60} \times 1000 \) mrad), arcsec (1 arcsec = \( \frac{\pi}{180 \times 3600} \times 1000 \) mrad), μrad (1 μrad = 0.001 mrad)

Steps:

Enter the object's height and the angular height observed through binoculars, and select their units.
Convert all inputs to base units (m for height, mrad for angular height).
Calculate the distance using \( d = \frac{h \times 1000}{\text{Mil}} \).
Convert the result to the selected unit (mm, cm, m, km, in, ft, yd, mi).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Binoculars Range Calculation

Calculating the distance using binoculars is crucial for:

Military Applications: Estimating the range to targets for tactical planning and artillery targeting.
Outdoor Activities: Determining distances in navigation, hunting, or wildlife observation.
Education: Understanding the use of angular measurements in practical ranging techniques.

4. Using the Calculator

Examples:

Example 1: For \( h = 6 \, \text{m} \), \( \text{Mil} = 1 \, \text{mrad} \), distance in m:
- Distance: \( d = \frac{6 \times 1000}{1} = 6000.0000 \, \text{m} \)
Example 2: For \( h = 10 \, \text{ft} \), \( \text{Mil} = 2 \, \text{mrad} \), distance in km:
- Convert: \( h = 10 \times 0.3048 = 3.048 \, \text{m} \)
- Distance: \( d = \frac{3.048 \times 1000}{2} = 1524.0000 \, \text{m} \)
- Convert to km: \( d = 1524.0000 \div 1000 = 1.5240 \, \text{km} \)

5. Frequently Asked Questions (FAQ)

Q: What is a milliradian (mrad)?
A: A milliradian is one-thousandth of a radian (0.001 rad). It is the angle subtended by 1 meter at a distance of 1 kilometer.

Q: How do I measure the angular height using binoculars?
A: Binoculars with a reticle (a scale in the field of view) allow you to estimate the angular height by comparing the object's apparent size to the reticle markings, typically in milliradians.

Q: Why is this method useful in the military?
A: It provides a quick and reliable way to estimate distances to targets without using electronic devices, which is essential for tactical operations and artillery aiming.