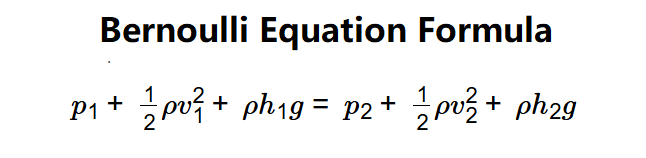Bernoulli Equation Calculator

Fluid Density Input Method:

Select Fluid:

Pressure at Point 1 (\( p_1 \)):

Pressure at Point 2 (\( p_2 \)):

Height at Point 1 (\( h_1 \)):

Height at Point 2 (\( h_2 \)):

Velocity at Point 1 (\( v_1 \)):

Velocity at Point 2 (\( v_2 \)):

Pressure Difference (\( \Delta p = p_2 - p_1 \)):

1. What is Bernoulli Equation Calculator?

Definition: This calculator uses the Bernoulli equation to compare two points along a streamline in a fluid flow, calculating the unknown velocity at the second point (\( v_2 \)) and the pressure difference (\( \Delta p = p_2 - p_1 \)).

Purpose: It is used in fluid dynamics to analyze the behavior of fluids in motion, such as in pipes, airfoils, or any system where the Bernoulli principle applies.

2. How Does the Calculator Work?

The calculator uses the Bernoulli equation:

\( p_1 + \frac{1}{2} \rho v_1^2 + \rho h_1 g = p_2 + \frac{1}{2} \rho v_2^2 + \rho h_2 g \)

Where:

\( \rho \): Density of the fluid (kg/m³);
\( p_1, p_2 \): Pressures at points 1 and 2 (Pa);
\( v_1, v_2 \): Velocities at points 1 and 2 (m/s);
\( h_1, h_2 \): Heights at points 1 and 2 (m);
\( g = 9.80665 \, \text{m/s}^2 \): Acceleration due to gravity;
\( \Delta p = p_2 - p_1 \): Pressure difference (Pa, can be negative).

Steps:

Choose the fluid density by selecting a fluid or entering a custom density with its unit.
Enter the pressures at points 1 and 2 (\( p_1, p_2 \)) with their units.
Enter the heights at points 1 and 2 (\( h_1, h_2 \)) with their units.
Enter the velocity at point 1 (\( v_1 \)) with its unit.
Convert all inputs to base units (kg/m³ for density, Pa for pressure, m for height, m/s for velocity).
Solve for \( v_2 \) by rearranging the Bernoulli equation: \( v_2 = \sqrt{\frac{p_1 - p_2 + \frac{1}{2} \rho v_1^2 + \rho g (h_1 - h_2)}{\frac{1}{2} \rho}} \).
Calculate the pressure difference: \( \Delta p = p_2 - p_1 \), which can be negative if \( p_2 < p_1 \).
Convert the results to the selected output units and display them, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Bernoulli Equation Calculation

The Bernoulli equation is crucial for:

Aerodynamics: Understanding lift on airplane wings and the behavior of airflow around objects.
Hydraulics: Designing pipelines, pumps, and turbines by analyzing pressure and velocity changes.
Fluid Dynamics Studies: Investigating the principles of fluid flow in various engineering and scientific applications.

4. Using the Calculator

Example 1 (Replicating the Image): Calculate \( v_2 \) and \( \Delta p \) for a fluid with the following properties:

Fluid Density: \( \rho = 1000 \, \text{kg/m}^3 \);
Pressure at Point 1: \( p_1 = 1000 \, \text{Pa} \);
Pressure at Point 2: \( p_2 = 1200 \, \text{Pa} \);
Height at Point 1: \( h_1 = 3 \, \text{m} \);
Height at Point 2: \( h_2 = 3 \, \text{m} \);
Velocity at Point 1: \( v_1 = 2 \, \text{m/s} \);
Using the Bernoulli equation: \( 1000 + 0.5 \times 1000 \times 2^2 + 1000 \times 3 \times 9.80665 = 1200 + 0.5 \times 1000 \times v_2^2 + 1000 \times 3 \times 9.80665 \);
Simplify: \( 1000 + 2000 = 1200 + 500 \times v_2^2 \);
Solve: \( v_2^2 = 3.6 \), so \( v_2 \approx 1.8974 \, \text{m/s} \);
Pressure Difference: \( \Delta p = 1200 - 1000 = 200 \, \text{Pa} \);
Result: \( v_2 = 1.8974 \, \text{m/s} \), \( \Delta p = 200.0000 \, \text{Pa} \).

Example 2 (Negative \( \Delta p \)): Calculate \( v_2 \) and \( \Delta p \) for air flowing with the following properties:

Fluid Density: \( \rho = 1.225 \, \text{kg/m}^3 \) (Air);
Pressure at Point 1: \( p_1 = 1.013 \, \text{bar} \);
Pressure at Point 2: \( p_2 = 0.9 \, \text{bar} \);
Height at Point 1: \( h_1 = 100 \, \text{ft} \);
Height at Point 2: \( h_2 = 90 \, \text{ft} \);
Velocity at Point 1: \( v_1 = 50 \, \text{mph} \);
Convert units: \( p_1 = 1.013 \times 10^5 = 101300 \, \text{Pa} \), \( p_2 = 0.9 \times 10^5 = 90000 \, \text{Pa} \), \( h_1 = 100 \times 0.3048 = 30.48 \, \text{m} \), \( h_2 = 90 \times 0.3048 = 27.432 \, \text{m} \), \( v_1 = 50 \times 0.44704 = 22.352 \, \text{m/s} \);
Using the Bernoulli equation: \( 101300 + 0.5 \times 1.225 \times 22.352^2 + 1.225 \times 30.48 \times 9.80665 = 90000 + 0.5 \times 1.225 \times v_2^2 + 1.225 \times 27.432 \times 9.80665 \);
Simplify: \( v_2 \approx 53.2517 \, \text{m/s} \);
Pressure Difference: \( \Delta p = 90000 - 101300 = -11300 \, \text{Pa} \);
Result (in selected units, e.g., mph, bar): \( v_2 = 119.0718 \, \text{mph} \), \( \Delta p = -0.1130 \, \text{bar} \).

5. Frequently Asked Questions (FAQ)

Q: What does a negative pressure difference mean?
A: A negative \( \Delta p \) (i.e., \( p_2 < p_1 \)) indicates that the pressure decreases from point 1 to point 2, which often corresponds to an increase in velocity due to the conservation of energy in the Bernoulli equation.

Q: Why does the velocity change with height?
A: The term \( \rho h g \) accounts for potential energy. If the height decreases (\( h_2 < h_1 \)), potential energy converts to kinetic energy, increasing the velocity, assuming other factors remain balanced.

Q: Can this calculator be used for compressible fluids?
A: The Bernoulli equation used here assumes an incompressible fluid. For compressible fluids (like gases at high speeds), a modified form of the equation is needed, which this calculator does not account for.