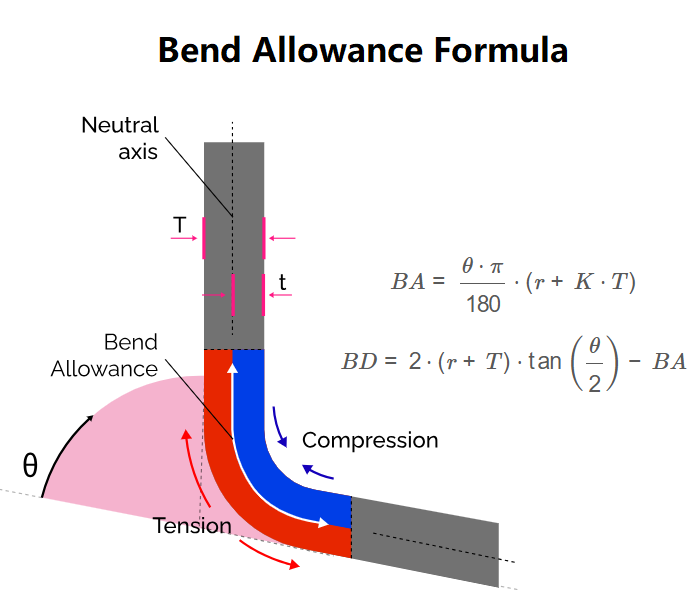
1. What is Bend Allowance and Deduction Calculator?
Definition: This calculator computes the bend allowance (\( BA \)), the length of the arc along the neutral axis of a bent material, and the bend deduction (\( BD \)), the amount to subtract from the total length to account for the bend.
Purpose: It is used in sheet metal fabrication to determine the flat length of a sheet metal piece before bending, ensuring accurate dimensions after the bending process.
2. How Does the Calculator Work?
The calculator uses the following formulas:
Formulas:
\[
BA = \frac{\theta \cdot \pi}{180} \cdot (r + K \cdot T)
\]
\[
BD = 2 \cdot (r + T) \cdot \tan\left(\frac{\theta}{2}\right) - BA
\]
Where:
- \( BA \): Bend allowance (mm, cm, dm, m, in, ft, yd)
- \( BD \): Bend deduction (mm, cm, dm, m, in, ft, yd)
- \( \theta \): Bend angle (deg, rad, gon, tr, arcmin, arcsec, mrad, μrad, x π rad)
- \( r \): Inside radius (mm, cm, dm, m, in, ft, yd)
- \( K \): K-factor (dimensionless, must be between 0 and 1)
- \( T \): Material thickness (mm, cm, dm, m, in, ft, yd)
Unit Conversions:
- Bend Allowance (\( BA \)), Bend Deduction (\( BD \)), Inside Radius (\( r \)), Material Thickness (\( T \)):
- 1 mm = 1 mm
- 1 cm = 10 mm
- 1 dm = 100 mm
- 1 m = 1000 mm
- 1 in = 25.4 mm
- 1 ft = 304.8 mm
- 1 yd = 914.4 mm
- Bend Angle (\( \theta \)):
- 1 deg = 1 deg
- 1 rad = \( \frac{180}{\pi} \) deg
- 1 gon = \( \frac{180}{200} \) deg
- 1 tr = 360 deg
- 1 arcmin = \( \frac{1}{60} \) deg
- 1 arcsec = \( \frac{1}{3600} \) deg
- 1 mrad = \( \frac{180}{\pi \times 1000} \) deg
- 1 μrad = \( \frac{180}{\pi \times 1000000} \) deg
- 1 x π rad = 180 deg
- K-factor (\( K \)): Dimensionless (must be between 0 and 1)
Steps:
- Enter the bend angle (\( \theta \)), inside radius (\( r \)), K-factor (\( K \)), and material thickness (\( T \)) with their respective units.
- Convert the bend angle to degrees and the length parameters to millimeters.
- Calculate \( BA = \frac{\theta \cdot \pi}{180} \cdot (r + K \cdot T) \).
- Calculate \( BD = 2 \cdot (r + T) \cdot \tan\left(\frac{\theta}{2}\right) - BA \).
- Convert the bend allowance and bend deduction to the selected units.
- Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
3. Importance of Bend Allowance and Deduction Calculation
Calculating the bend allowance and deduction is crucial for:
- Sheet Metal Fabrication: Determining the flat length of a sheet before bending to achieve accurate final dimensions.
- Manufacturing: Ensuring precise cuts and bends in metalworking processes.
- Design: Creating components that fit together correctly after bending.
4. Using the Calculator
Examples:
- Example 1: For \( \theta = 90 \, \text{deg} \), \( r = 10 \, \text{mm} \), \( K = 0.5 \), \( T = 2 \, \text{mm} \), bend allowance and deduction in millimeters:
- \( BA = \frac{90 \cdot \pi}{180} \cdot (10 + 0.5 \cdot 2) \)
- \( BA = \frac{\pi}{2} \cdot (10 + 1) \approx 1.5708 \cdot 11 \approx 17.2788 \, \text{mm} \)
- \( BD = 2 \cdot (10 + 2) \cdot \tan\left(\frac{90}{2}\right) - 17.2788 \)
- \( BD = 2 \cdot 12 \cdot \tan(45^\circ) - 17.2788 \approx 24 \cdot 1 - 17.2788 \approx 6.7212 \, \text{mm} \)
- Example 2: For \( \theta = 1 \, \text{rad} \), \( r = 0.5 \, \text{in} \), \( K = 0.4 \), \( T = 0.1 \, \text{in} \), bend allowance and deduction in inches:
- Convert: \( \theta = 1 \times \frac{180}{\pi} \approx 57.2958 \, \text{deg} \), \( r = 0.5 \times 25.4 = 12.7 \, \text{mm} \), \( T = 0.1 \times 25.4 = 2.54 \, \text{mm} \)
- \( BA = \frac{57.2958 \cdot \pi}{180} \cdot (12.7 + 0.4 \cdot 2.54) \)
- \( BA \approx 1 \cdot (12.7 + 1.016) \approx 13.716 \, \text{mm} \)
- \( BD = 2 \cdot (12.7 + 2.54) \cdot \tan\left(\frac{57.2958}{2}\right) - 13.716 \)
- \( BD \approx 2 \cdot 15.24 \cdot \tan(28.6479^\circ) - 13.716 \approx 30.48 \cdot 0.5412 - 13.716 \approx 2.7965 \, \text{mm} \)
- Convert to inches: \( BA \approx 13.716 / 25.4 \approx 0.5402 \, \text{in} \), \( BD \approx 2.7965 / 25.4 \approx 0.1101 \, \text{in} \)
5. Frequently Asked Questions (FAQ)
Q: What is bend allowance?
A: Bend allowance is the length of the arc along the neutral axis of a bent material, used to calculate the flat length of a sheet before bending.
Q: What is bend deduction?
A: Bend deduction is the amount to subtract from the total length of a sheet to account for the bend, ensuring the correct final dimensions after bending.
Q: What is the K-factor?
A: The K-factor is a ratio that represents the location of the neutral axis relative to the material thickness, typically between 0 and 1.
Q: How are bend allowance and deduction used in real life?
A: They are used in sheet metal fabrication to determine the flat dimensions of a part before bending, ensuring accurate final shapes in manufacturing. It is advisable to consult your supplier for specific information.
Bend Allowance and Deduction Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back