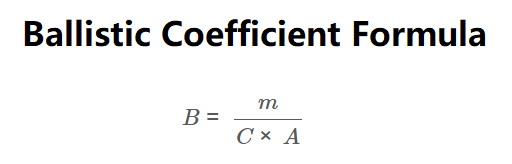Ballistic Coefficient Calculator

Mass of Projectile:

Drag Coefficient (C):

Area of Cross-Section (A):

1. What is a Ballistic Coefficient Calculator?

Definition: This calculator determines the ballistic coefficient of a projectile, which measures its ability to overcome air resistance while traveling.

Purpose: It is used by shooters, hunters, and ballistics enthusiasts to evaluate the aerodynamic efficiency of projectiles, aiding in trajectory predictions and performance optimization.

2. How Does the Calculator Work?

The calculator uses the following formula:

\[ B = \frac{m}{C \times A} \] Where:

\(B\): Ballistic coefficient (kg/m² or lbs/in²)
\(m\): Mass of the projectile (g, kg, gr, oz, lb)
\(C\): Drag coefficient (dimensionless)
\(A\): Cross-sectional area of the projectile (mm², cm², m², in²)

Unit Conversions:

Output Units: kg/m², lbs/in²

Steps:

Enter the mass of the projectile, selecting the unit (g, kg, gr, oz, lb)
Enter the drag coefficient (C), which is dimensionless
Enter the cross-sectional area of the projectile, selecting the unit (mm², cm², m², in²)
Convert all inputs to consistent units (kg for mass, m² for area)
Calculate the ballistic coefficient using the formula
Select the desired unit for the result and view the converted value

3. Importance of Ballistic Coefficient Calculation

The ballistic coefficient is crucial for understanding a projectile's performance:

Aerodynamic Efficiency: A higher ballistic coefficient indicates better ability to overcome air resistance, leading to flatter trajectories and less wind drift.
Accuracy: Helps in predicting the projectile's path, improving accuracy over long distances.
Hunting and Shooting: Essential for selecting the right projectile for specific applications, such as hunting or competitive shooting.

4. Using the Calculator

Examples:

Example 1: For a projectile with mass \(m = 50 \, \text{g}\), drag coefficient \(C = 0.295\), and cross-sectional area \(A = 45.6 \, \text{mm}^2\):
- Mass in kg = \(50 \, \text{g} = 0.05 \, \text{kg}\)
- Area in m² = \(45.6 \, \text{mm}^2 = 4.56 \times 10^{-5} \, \text{m}^2\)
- Ballistic coefficient = \(\frac{0.05}{0.295 \times 4.56 \times 10^{-5}} = 3718.171 \, \text{kg/m}^2\)
Example 2: For a projectile with mass \(m = 0.1 \, \text{lb}\), drag coefficient \(C = 0.3\), and cross-sectional area \(A = 0.196 \, \text{in}^2\):
- Mass in kg = \(0.1 \, \text{lb} = 0.0453592 \, \text{kg}\)
- Area in m² = \(0.196 \, \text{in}^2 = 1.266 \times 10^{-4} \, \text{m}^2\)
- Ballistic coefficient = \(\frac{0.0453592}{0.3 \times 1.266 \times 10^{-4}} = 1193.674 \, \text{kg/m}^2\)
- In lbs/in² = \(1193.674 \times 0.00142233 = 1.698 \, \text{lbs/in}^2\)

5. Frequently Asked Questions (FAQ)

Q: What is the ballistic coefficient?
A: The ballistic coefficient measures a projectile's ability to overcome air resistance, calculated as \(B = m / (C \times A)\).

Q: What is the G1 model?
A: The G1 model is a standard drag model used for flat base and ogive nose projectiles, commonly used to define ballistic coefficients in shooting.

Q: Why is the drag coefficient important?
A: The drag coefficient (C) quantifies the aerodynamic drag on the projectile, directly affecting the ballistic coefficient and flight performance.