1. What is Buoyancy Force Calculator?

Definition: This calculator computes the buoyant force (\( F_B \)) acting on an object fully immersed in a fluid, based on Archimedes' Principle.

Purpose: It is used in physics and engineering to determine the upward force exerted by a fluid on a submerged object, which helps in understanding whether an object will float, sink, or remain neutrally buoyant.

2. How Does the Calculator Work?

The calculator follows these steps based on Archimedes' Principle:

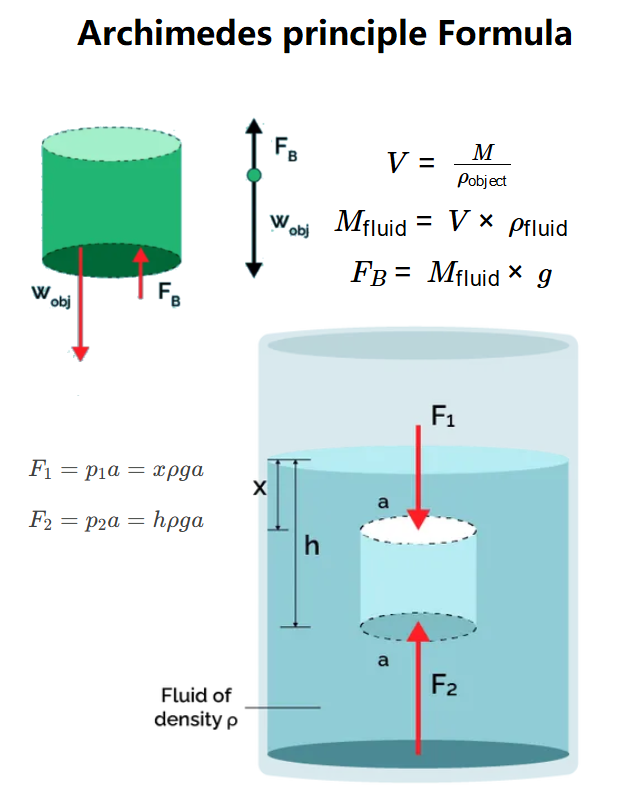
• \( V = \frac{M}{\rho_{\text{object}}} \)
• \( M_{\text{fluid}} = V \times \rho_{\text{fluid}} \)
• \( F_B = M_{\text{fluid}} \times g \)

Where:

• \( M \): Mass of the object (kg);
• \( \rho_{\text{object}} \): Density of the object (kg/m³);
• \( V \): Volume of the object (m³), also the volume of displaced fluid since the object is fully immersed;
• \( \rho_{\text{fluid}} \): Density of the fluid (kg/m³);
• \( M_{\text{fluid}} \): Mass of the displaced fluid (kg);
• \( g = 9.8 \, \text{m/s}^2 \): Acceleration due to gravity;
• \( F_B \): Buoyant force (N).

Steps:

• Enter the mass of the object and select its unit.
• Choose the object's density by selecting a material or manually entering the density with its unit.
• Choose the fluid's density by selecting a fluid or manually entering the density with its unit.
• Convert all inputs to base units (kg for mass, kg/m³ for density).
• Calculate the volume of the object using \( V = \frac{M}{\rho_{\text{object}}} \).
• Calculate the mass of the displaced fluid using \( M_{\text{fluid}} = V \times \rho_{\text{fluid}} \).
• Calculate the buoyant force using \( F_B = M_{\text{fluid}} \times g \).
• Convert the results to the selected output units and display them, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Buoyancy Force Calculation

Calculating the buoyant force is crucial for:

• Floatation Analysis: Determining whether an object will float or sink in a fluid, which is essential for designing ships, submarines, and buoys.
• Engineering Applications: Understanding the forces acting on submerged structures like pipelines or underwater equipment.
• Physics Experiments: Studying the principles of fluid mechanics and buoyancy in educational settings.

4. Using the Calculator

Example 1 (Dropdown): Calculate the buoyant force for an aluminum block with mass 1.00 × 10⁶ kg fully immersed in water (replicating the example from the image):

• Mass: \( 1.00 \times 10^6 \, \text{kg} \);
• Object Density (Aluminum): \( \rho_{\text{object}} = 2700 \, \text{kg/m}^3 \);
• Fluid Density (Water): \( \rho_{\text{fluid}} = 1000 \, \text{kg/m}^3 \);
• Volume: \( V = \frac{M}{\rho_{\text{object}}} = \frac{1.00 \times 10^6}{2700} \approx 370.3704 \, \text{m}^3 \);
• Mass of Displaced Fluid: \( M_{\text{fluid}} = V \times \rho_{\text{fluid}} = 370.3704 \times 1000 = 3.70 \times 10^5 \, \text{kg} \);
• Buoyant Force: \( F_B = M_{\text{fluid}} \times g = 3.70 \times 10^5 \times 9.8 = 3.63 \times 10^6 \, \text{N} \);
• Result (in selected units, e.g., m³, kg, N): \( V = 370.3704 \, \text{m}^3 \), \( M_{\text{fluid}} = 370370.3704 \, \text{kg} \), \( F_B = 3629629.6296 \, \text{N} \).

Example 2 (Manual Input with Different Units): Calculate the buoyant force for a steel object with mass 500 lb and density 489.9 lb/cu ft fully immersed in seawater (density 1.025 g/cm³):

• Mass: \( 500 \, \text{lb} = 500 \times 0.453592 = 226.796 \, \text{kg} \);
• Object Density: \( \rho_{\text{object}} = 489.9 \, \text{lb/cu ft} = 489.9 \times 16.0185 = 7847.4632 \, \text{kg/m}^3 \);
• Fluid Density: \( \rho_{\text{fluid}} = 1.025 \, \text{g/cm}^3 = 1.025 \times 1000 = 1025 \, \text{kg/m}^3 \);
• Volume: \( V = \frac{M}{\rho_{\text{object}}} = \frac{226.796}{7847.4632} \approx 0.0289 \, \text{m}^3 \);
• Mass of Displaced Fluid: \( M_{\text{fluid}} = V \times \rho_{\text{fluid}} = 0.0289 \times 1025 \approx 29.6225 \, \text{kg} \);
• Buoyant Force: \( F_B = M_{\text{fluid}} \times g = 29.6225 \times 9.8 \approx 290.3005 \, \text{N} \);
• Result (in selected units, e.g., cm³, lb, lbf): \( V = 28900.0000 \, \text{cm}^3 \), \( M_{\text{fluid}} = 65.3015 \, \text{lb} \), \( F_B = 65.2691 \, \text{lbf} \).

5. Frequently Asked Questions (FAQ)

Q: What happens if the object is not fully immersed?
A: This calculator assumes the object is fully immersed. If the object is partially immersed, you would need to calculate the volume of the submerged portion and use that to determine the displaced fluid mass.

Q: Why does the buoyant force depend on the fluid density?
A: The buoyant force is proportional to the mass of the displaced fluid, which depends on the fluid's density. A denser fluid will displace more mass for the same volume, resulting in a greater buoyant force.

Q: Can this calculator be used for gases?
A: Yes, the principle applies to any fluid, including gases. However, the density of gases is much lower than liquids, so the buoyant force will be significantly smaller.

Buoyancy Force Calculator© - All Rights Reserved 2025