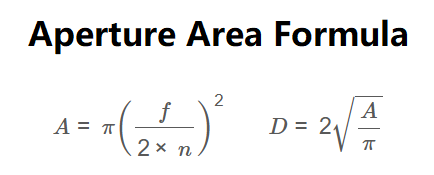Aperture Area Calculator

Aperture Area (\( A \)):

Aperture Diameter (\( D \)):

1. What is an Aperture Area Calculator?

Definition: This calculator computes the aperture area (\( A \)) and aperture diameter (\( D \)) of a lens using the focal length and f-number.

Purpose: It is used in optics to determine the effective area and diameter of a lens aperture, which affect the amount of light entering the optical system and its resolving power.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Aperture Area: \[ A = \pi \left( \frac{f}{2 \times n} \right)^2 \] Aperture Diameter: \[ D = 2 \sqrt{\frac{A}{\pi}} \] Where:

\( A \): Aperture area (mm², cm², m², km², in², ft², yd², mi²)
\( D \): Aperture diameter (mm, cm, m, km, in, ft, yd, mi)
\( f \): Focal length (mm, cm, m, km, in, ft, yd, mi)
\( n \): F-Number (dimensionless)

Unit Conversions:

Focal Length (\( f \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, km (1 km = 1000 m), in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m), mi (1 mi = 1609.344 m)
Aperture Area (\( A \)): mm² (1 m² = \( 10^6 \) mm²), cm² (1 m² = \( 10^4 \) cm²), m², km² (1 m² = \( 10^{-6} \) km²), in² (1 m² = \( \frac{1}{(0.0254)^2} \) in²), ft² (1 m² = \( \frac{1}{(0.3048)^2} \) ft²), yd² (1 m² = \( \frac{1}{(0.9144)^2} \) yd²), mi² (1 m² = \( \frac{1}{(1609.344)^2} \) mi²)
Aperture Diameter (\( D \)): mm (1 m = 1000 mm), cm (1 m = 100 cm), m, km (1 m = 0.001 km), in (1 m = \( \frac{1}{0.0254} \) in), ft (1 m = \( \frac{1}{0.3048} \) ft), yd (1 m = \( \frac{1}{0.9144} \) yd), mi (1 m = \( \frac{1}{1609.344} \) mi)

Steps:

Enter the focal length and f-number, and select the unit for focal length.
Convert the focal length to base units (m).
Calculate the aperture area using \( A = \pi \left( \frac{f}{2 \times n} \right)^2 \).
Calculate the aperture diameter using \( D = 2 \sqrt{\frac{A}{\pi}} \).
Convert the results to the selected units (area: mm², cm², m², km², in², ft², yd², mi²; diameter: mm, cm, m, km, in, ft, yd, mi).
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Aperture Area and Diameter Calculation

Calculating the aperture area and diameter is crucial for:

Optics Education: Understanding the relationship between aperture size, light collection, and image quality.
Photography: Determining the light-gathering capability of a lens, which affects exposure and depth of field.
Astronomy: Evaluating the performance of telescopes in collecting light from distant objects.

4. Using the Calculator

Examples:

Example 1: For \( f = 70 \, \text{mm} \), \( n = 1.4 \), aperture area in mm², diameter in mm:
- Convert: \( f = 70 \times 0.001 = 0.07 \, \text{m} \)
- Aperture Area: \( A = \pi \left( \frac{0.07}{2 \times 1.4} \right)^2 = \pi \times \left( \frac{0.07}{2.8} \right)^2 = \pi \times (0.025)^2 \approx 0.0019635 \, \text{m}^2 \)
- Convert to mm²: \( A = 0.0019635 \times 10^6 = 1963.5000 \, \text{mm}^2 \)
- Aperture Diameter: \( D = 2 \sqrt{\frac{0.0019635}{\pi}} \approx 2 \sqrt{0.000625} = 2 \times 0.025 = 0.05 \, \text{m} = 50.0000 \, \text{mm} \)
Example 2: For \( f = 50 \, \text{mm} \), \( n = 2 \), aperture area in cm², diameter in cm:
- Convert: \( f = 50 \times 0.001 = 0.05 \, \text{m} \)
- Aperture Area: \( A = \pi \left( \frac{0.05}{2 \times 2} \right)^2 = \pi \times \left( \frac{0.05}{4} \right)^2 = \pi \times (0.0125)^2 \approx 0.0004909 \, \text{m}^2 \)
- Convert to cm²: \( A = 0.0004909 \times 10^4 = 4.9087 \, \text{cm}^2 \)
- Aperture Diameter: \( D = 2 \sqrt{\frac{0.0004909}{\pi}} \approx 2 \sqrt{0.00015625} = 2 \times 0.0125 = 0.025 \, \text{m} = 2.5000 \, \text{cm} \)

5. Frequently Asked Questions (FAQ)

Q: What is aperture area?
A: Aperture area is the effective area of a lens opening through which light passes, affecting the lens's light-gathering capability and resolution.

Q: How does the f-number relate to aperture area and diameter?
A: The f-number (\( n \)) is the ratio of the focal length to the aperture diameter. A smaller f-number means a larger aperture diameter and thus a larger aperture area, allowing more light to enter.

Q: Why are aperture area and diameter important in photography?
A: They determine the amount of light entering the camera, impacting exposure, depth of field, and image brightness.