Antenna Downtilt Coverage Radius Calculator

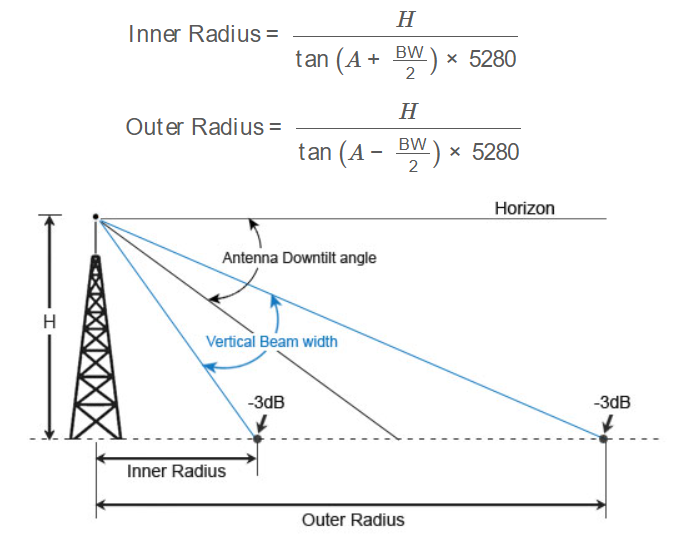
Antenna Downtilt Coverage Radius Formula

1. What is Antenna Downtilt Coverage Radius Calculator?

Definition: This calculator determines the inner and outer coverage radii of an antenna's beam based on the tower height, downtilt angle, and vertical beamwidth.

Purpose: It is used in RF engineering and telecommunications to optimize antenna coverage in cellular networks, ensuring signals cover the intended area effectively.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ \text{Inner Radius} = \frac{H}{\tan\left(A + \frac{\text{BW}}{2}\right) \times 5280} \] \[ \text{Outer Radius} = \frac{H}{\tan\left(A - \frac{\text{BW}}{2}\right) \times 5280} \] Where:

\( \text{Inner Radius}, \text{Outer Radius} \): Coverage radii (mi, km, m, ft)
\( H \): Tower Height (ft)
\( A \): Downtilt Angle (degrees)
\( \text{BW} \): Vertical Beamwidth (degrees)

Unit Conversions:

Tower Height:
- 1 ft = 1 foot
- 1 m = 3.28084 ft
- 1 km = 3280.84 ft
- 1 mi = 5280 ft
Inner/Outer Coverage Radius:
- 1 mi = 1 mile
- 1 km = 0.621371 mi
- 1 m = 0.000621371 mi
- 1 ft = 0.000189394 mi
Downtilt Angle, Vertical Beamwidth: Measured in degrees, no conversion needed

Steps:

Enter the Tower Height (positive value) and select the unit (ft, m, km, mi).
Enter the Downtilt Angle in degrees.
Enter the Vertical Beamwidth in degrees (between 0 and 180).
Convert Tower Height to feet.
Calculate Inner and Outer Radii in miles using the formulas.
Convert the results to the selected unit.
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Antenna Downtilt Coverage Radius Calculation

Calculating the Antenna Downtilt Coverage Radius is crucial for:

RF Engineering: Determining the coverage area to reduce interference and improve signal quality.
Telecommunications: Ensuring base stations cover the intended area effectively, especially in urban environments.
Network Planning: Enhancing network performance by defining precise coverage zones.

4. Using the Calculator

Examples:

Example 1: For \( H = 100 \, \text{ft} \), \( A = 5 \, \text{degrees} \), \( \text{BW} = 6 \, \text{degrees} \), results in miles:
- Inner angle: \( 5 + \frac{6}{2} = 8 \, \text{degrees} \)
- Outer angle: \( 5 - \frac{6}{2} = 2 \, \text{degrees} \)
- \( \text{Inner Radius} = \frac{100}{\tan(8^\circ) \times 5280} \approx 0.0045 \, \text{mi} \)
- \( \text{Outer Radius} = \frac{100}{\tan(2^\circ) \times 5280} \approx 0.0181 \, \text{mi} \)
Example 2: For \( H = 30.48 \, \text{m} \), \( A = 3 \, \text{degrees} \), \( \text{BW} = 4 \, \text{degrees} \), results in kilometers:
- Convert to feet: \( H = 30.48 \times 3.28084 = 100 \, \text{ft} \)
- Inner angle: \( 3 + \frac{4}{2} = 5 \, \text{degrees} \)
- Outer angle: \( 3 - \frac{4}{2} = 1 \, \text{degree} \)
- \( \text{Inner Radius} = \frac{100}{\tan(5^\circ) \times 5280} \approx 0.0071 \, \text{mi} \)
- \( \text{Outer Radius} = \frac{100}{\tan(1^\circ) \times 5280} \approx 0.0356 \, \text{mi} \)
- Convert to kilometers: \( \text{Inner Radius} \approx 0.0115 \, \text{km} \), \( \text{Outer Radius} \approx 0.0573 \, \text{km} \)

5. Frequently Asked Questions (FAQ)

Q: What are inner and outer coverage radii?
A: The inner radius is the distance where the upper edge of the antenna beam hits the ground, and the outer radius is where the lower edge hits, defining the coverage area.

Q: Why is vertical beamwidth important?
A: Vertical beamwidth determines the angular spread of the antenna's main lobe, affecting the size of the coverage area.

Q: How is this calculation used in real life?
A: It is used in cellular network planning to define coverage zones, reduce interference, and ensure optimal signal distribution.