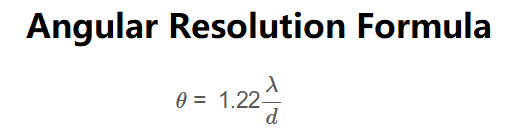Angular Resolution Calculator

Wavelength (\( \lambda \)):

Diameter of Lens Aperture (\( d \)):

1. What is an Angular Resolution Calculator?

Definition: This calculator computes the angular resolution (\( \theta \)) of an optical system using the Rayleigh criterion, which determines the minimum angular separation at which two point sources can be distinguished.

Purpose: It is used in optics to evaluate the resolving power of telescopes, microscopes, and other optical instruments, helping to understand their ability to distinguish fine details.

2. How Does the Calculator Work?

The calculator uses the Rayleigh criterion formula for angular resolution:

Angular Resolution: \[ \theta = 1.22 \frac{\lambda}{d} \] Where:

\( \theta \): Angular resolution (rad, deg, arcmin, arcsec, mrad, μrad)
\( \lambda \): Wavelength of light (nm, μm, mm, cm, m, km, in, ft, yd, mi)
\( d \): Diameter of the lens aperture (mm, cm, m, km, in, ft, yd, mi)

Unit Conversions:

Wavelength (\( \lambda \)): nm (1 nm = \( 10^{-9} \) m), μm (1 μm = \( 10^{-6} \) m), mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, km (1 km = 1000 m), in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m), mi (1 mi = 1609.344 m)
Diameter (\( d \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, km (1 km = 1000 m), in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m), mi (1 mi = 1609.344 m)
Angular Resolution (\( \theta \)): rad, deg (1 rad = \( \frac{180}{\pi} \) deg), arcmin (1 rad = \( \frac{180}{\pi} \times 60 \) arcmin), arcsec (1 rad = \( \frac{180}{\pi} \times 3600 \) arcsec), mrad (1 rad = 1000 mrad), μrad (1 rad = \( 10^6 \) μrad)

Steps:

Enter the wavelength of light and the diameter of the lens aperture, and select their units.
Convert all inputs to base units (m for both wavelength and diameter).
Calculate the angular resolution using \( \theta = 1.22 \frac{\lambda}{d} \).
Convert the result to the selected unit (rad, deg, arcmin, arcsec, mrad, or μrad).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Angular Resolution Calculation

Calculating the angular resolution is crucial for:

Optics Education: Understanding the limits of resolution in optical systems due to diffraction.
Astronomy: Determining the ability of telescopes to resolve distant stars or celestial objects.
Microscopy: Evaluating the resolving power of microscopes to distinguish fine details in samples.

4. Using the Calculator

Examples:

Example 1: For \( \lambda = 550 \, \text{nm} \), \( d = 50 \, \text{mm} \), angular resolution in rad:
- Convert: \( \lambda = 550 \times 10^{-9} = 5.5 \times 10^{-7} \, \text{m} \), \( d = 50 \times 0.001 = 0.05 \, \text{m} \)
- Angular Resolution: \( \theta = 1.22 \times \frac{5.5 \times 10^{-7}}{0.05} = 1.22 \times 1.1 \times 10^{-5} = 1.3420 \times 10^{-5} \, \text{rad} \)
Example 2: For \( \lambda = 500 \, \text{nm} \), \( d = 2 \, \text{in} \), angular resolution in arcsec:
- Convert: \( \lambda = 500 \times 10^{-9} = 5.0 \times 10^{-7} \, \text{m} \), \( d = 2 \times 0.0254 = 0.0508 \, \text{m} \)
- Angular Resolution: \( \theta = 1.22 \times \frac{5.0 \times 10^{-7}}{0.0508} \approx 1.22 \times 9.8425 \times 10^{-6} \approx 1.2008 \times 10^{-5} \, \text{rad} \)
- Convert to arcsec: \( \theta = 1.2008 \times 10^{-5} \times \frac{180}{\pi} \times 3600 \approx 2.4752 \, \text{arcsec} \)

5. Frequently Asked Questions (FAQ)

Q: What is angular resolution?
A: Angular resolution, also known as the Rayleigh criterion, is the minimum angular separation at which two point sources can be distinguished by an optical system, limited by diffraction.

Q: Why does angular resolution depend on wavelength and aperture size?
A: Shorter wavelengths and larger apertures reduce diffraction effects, allowing for finer resolution of details.

Q: What is the significance of the Rayleigh criterion in real life?
A: It determines the resolving power of optical instruments like telescopes and microscopes, affecting their ability to distinguish closely spaced objects, such as stars in astronomy or cells in biology.