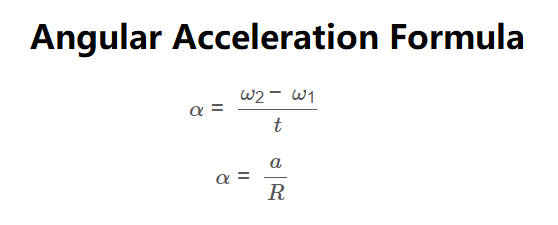1. What is an Angular Acceleration Calculator?

Definition: This calculator determines the angular acceleration of an object, either by using the change in angular velocity over time or by using tangential acceleration and radius.

Purpose: It is used in physics to analyze rotational motion, such as in rotating machinery, wheels, or celestial bodies.

2. How Does the Calculator Work?

The calculator supports two methods to calculate angular acceleration:

1. Using Angular Velocities: \[ \alpha = \frac{\omega_2 - \omega_1}{t} \] 2. Using Tangential Acceleration: \[ \alpha = \frac{a}{R} \] Where:

• \( \alpha \): Angular acceleration (rad/s²)
• \( \omega_1 \): Initial angular velocity (rpm, rad/s, Hz)
• \( \omega_2 \): Final angular velocity (rpm, rad/s, Hz)
• \( t \): Time (sec, min, hr, days, wks, mos, yrs)
• \( a \): Tangential acceleration (m/s²)
• \( R \): Radius (mm, cm, m, km, in, ft, yd)

Unit Conversions:

• Angular Velocity (\( \omega_1 \), \( \omega_2 \)): rpm (1 rpm = \( \frac{2\pi}{60} \) rad/s ≈ 0.104719755 rad/s), rad/s, Hz (1 Hz = \( 2\pi \) rad/s ≈ 6.283185307 rad/s)
• Time (\( t \)): sec, min (1 min = 60 s), hr (1 hr = 3600 s), days (1 day = 86400 s), wks (1 wk = 604800 s), mos (1 mo = 2628000 s), yrs (1 yr = 31536000 s)
• Tangential Acceleration (\( a \)): m/s²
• Radius (\( R \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, km (1 km = 1000 m), in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
• Angular Acceleration (\( \alpha \)): rad/s²

Steps:

• Select the calculation mode (Using Angular Velocities or Using Tangential Acceleration).
• Enter the required values and select their units (initial and final angular velocities and time, or tangential acceleration and radius).
• Convert all inputs to base units (rad/s, s, m/s², m).
• Calculate the angular acceleration using the selected formula.
• If the result is less than 0.001, display it in scientific notation; otherwise, display it with 3 decimal places.

3. Importance of Angular Acceleration Calculation

Calculating angular acceleration is crucial for:

• Physics Education: Understanding rotational dynamics.
• Engineering: Designing rotating machinery like engines and turbines.
• Astronomy: Analyzing the motion of celestial bodies.

4. Using the Calculator

Examples:

• Example 1 (Using Angular Velocities): For \( \omega_1 = 120 \, \text{rpm} \), \( \omega_2 = 600 \, \text{rpm} \), \( t = 4 \, \text{s} \):
  • Convert: \( \omega_1 = 120 \times \frac{2\pi}{60} = 12.566 \, \text{rad/s} \), \( \omega_2 = 600 \times \frac{2\pi}{60} = 62.832 \, \text{rad/s} \)
  • Angular Acceleration: \( \alpha = \frac{62.832 - 12.566}{4} = 12.566 \, \text{rad/s²} \)
• Example 2 (Using Angular Velocities with Different Time Unit): For \( \omega_1 = 0 \, \text{rad/s} \), \( \omega_2 = 2 \, \text{Hz} \), \( t = 1 \, \text{min} \):
  • Convert: \( \omega_2 = 2 \times 2\pi = 12.566 \, \text{rad/s} \), \( t = 1 \times 60 = 60 \, \text{s} \)
  • Angular Acceleration: \( \alpha = \frac{12.566 - 0}{60} = 0.209 \, \text{rad/s²} \)
• Example 3 (Using Tangential Acceleration): For \( a = 5 \, \text{m/s²} \), \( R = 200 \, \text{cm} \):
  • Convert: \( R = 200 \times 0.01 = 2 \, \text{m} \)
  • Angular Acceleration: \( \alpha = \frac{5}{2} = 2.500 \, \text{rad/s²} \)
• Example 4 (Small Value with Scientific Notation): For \( \omega_1 = 0 \, \text{rad/s} \), \( \omega_2 = 0.0001 \, \text{rad/s} \), \( t = 100 \, \text{s} \):
  • Angular Acceleration: \( \alpha = \frac{0.0001 - 0}{100} = 0.000001 \)
  • Since 0.000001 < 0.001, display as \( 1.000 \times 10^{-6} \, \text{rad/s²} \)

5. Frequently Asked Questions (FAQ)

Q: What is angular acceleration?
A: Angular acceleration is the rate of change of angular velocity over time, measured in rad/s².

Q: How is angular acceleration related to tangential acceleration?
A: Angular acceleration is related to tangential acceleration by the formula \( \alpha = \frac{a}{R} \), where \( a \) is the tangential acceleration and \( R \) is the radius.

Q: Can angular acceleration be negative?
A: Yes, a negative angular acceleration indicates a decrease in angular velocity (deceleration).

Angular Acceleration Calculator© - All Rights Reserved 2025