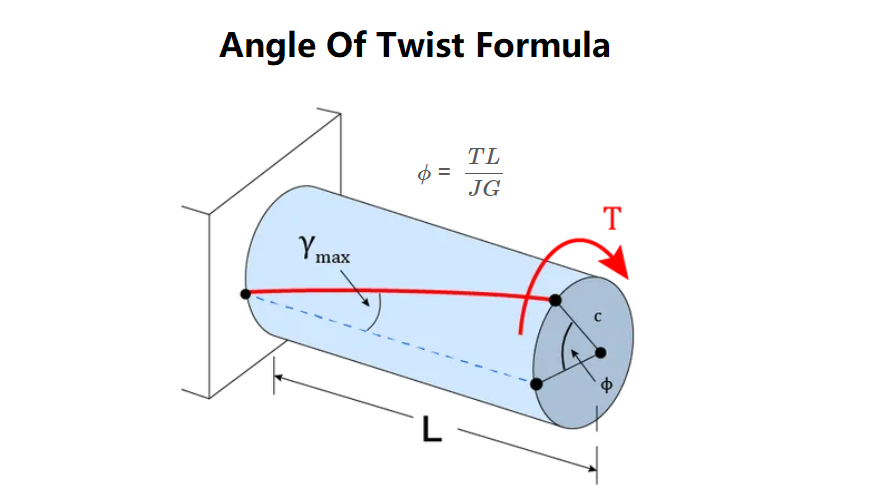
1. What is Angle of Twist Calculator?
Definition: This calculator computes the angle of twist (\( \phi \)), the relative rotation of one end of a shaft with respect to the other when a torque is applied.
Purpose: It is used in mechanical engineering to analyze the torsional deformation of shafts and to ensure that the deformation remains within acceptable limits for design purposes.
2. How Does the Calculator Work?
The calculator uses the following formula:
Formula:
\[
\phi = \frac{TL}{JG}
\]
Where:
- \( \phi \): Angle of twist (deg, rad, gon, tr, arcmin, arcsec, mrad, μrad, x π rad)
- \( T \): Internal torque (N·m, N·mm, kN·m, lbf·ft, lbf·in)
- \( L \): Shaft length (mm, cm, dm, m, in, ft, yd)
- \( J \): Polar moment of inertia (mm⁴, cm⁴, m⁴, in⁴, ft⁴)
- \( G \): Shear modulus (Pa, kPa, MPa, GPa, psi, ksi)
Unit Conversions:
- Torque (\( T \)):
- 1 N·m = 1 N·m
- 1 N·mm = 0.001 N·m
- 1 kN·m = 1000 N·m
- 1 lbf·ft = 1.35582 N·m
- 1 lbf·in = 0.112985 N·m
- Length (\( L \)):
- 1 mm = 0.001 m
- 1 cm = 0.01 m
- 1 dm = 0.1 m
- 1 m = 1 m
- 1 in = 0.0254 m
- 1 ft = 0.3048 m
- 1 yd = 0.9144 m
- Polar Moment of Inertia (\( J \)):
- 1 mm⁴ = 1e-12 m⁴
- 1 cm⁴ = 1e-8 m⁴
- 1 m⁴ = 1 m⁴
- 1 in⁴ = 4.162314e-7 m⁴
- 1 ft⁴ = 0.00863097 m⁴
- Shear Modulus (\( G \)):
- 1 Pa = 1 Pa
- 1 kPa = 1e3 Pa
- 1 MPa = 1e6 Pa
- 1 GPa = 1e9 Pa
- 1 psi = 6894.76 Pa
- 1 ksi = 6894760 Pa
- Angle (\( \phi \)):
- 1 deg = \( \frac{\pi}{180} \) rad
- 1 rad = 1 rad
- 1 gon = \( \frac{\pi}{200} \) rad
- 1 tr = \( 2\pi \) rad
- 1 arcmin = \( \frac{\pi}{180 \times 60} \) rad
- 1 arcsec = \( \frac{\pi}{180 \times 3600} \) rad
- 1 mrad = 0.001 rad
- 1 μrad = 0.000001 rad
- 1 x π rad = \( x \times \pi \) rad
Steps:
- Enter the internal torque (\( T \)), shaft length (\( L \)), polar moment of inertia (\( J \)), and shear modulus (\( G \)) with their respective units.
- Convert all inputs to SI units (N·m, m, m⁴, Pa).
- Calculate \( \phi = \frac{TL}{JG} \) in radians.
- Convert the angle to the selected unit.
- Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
3. Importance of Angle of Twist Calculation
Calculating the angle of twist is crucial for:
- Mechanical Engineering: Designing shafts and ensuring they can withstand torsional loads without excessive deformation.
- Structural Analysis: Analyzing the behavior of rotating machinery components like axles and drive shafts.
- Material Selection: Choosing materials with appropriate shear modulus for specific applications.
4. Using the Calculator
Examples:
- Example 1: For \( T = 1000 \, \text{N·m} \), \( L = 2 \, \text{m} \), \( J = 0.0001 \, \text{m⁴} \), \( G = 80 \, \text{GPa} \), angle in degrees:
- Convert: \( G = 80 \times 10^9 = 8 \times 10^{10} \, \text{Pa} \)
- \( \phi = \frac{1000 \times 2}{0.0001 \times 8 \times 10^{10}} = 0.00025 \, \text{rad} \)
- Convert to degrees: \( \phi = 0.00025 \times \frac{180}{\pi} \approx 0.0143^\circ \)
- Example 2: For \( T = 500 \, \text{lbf·ft} \), \( L = 3 \, \text{ft} \), \( J = 2 \, \text{in⁴} \), \( G = 11.5 \, \text{ksi} \), angle in radians:
- Convert: \( T = 500 \times 1.35582 = 677.91 \, \text{N·m} \), \( L = 3 \times 0.3048 = 0.9144 \, \text{m} \), \( J = 2 \times 4.162314 \times 10^{-7} = 8.324628 \times 10^{-7} \, \text{m⁴} \), \( G = 11.5 \times 6894760 = 7.928974 \times 10^7 \, \text{Pa} \)
- \( \phi = \frac{677.91 \times 0.9144}{8.324628 \times 10^{-7} \times 7.928974 \times 10^7} \approx 0.0094 \, \text{rad} \)
5. Frequently Asked Questions (FAQ)
Q: What is the angle of twist?
A: The angle of twist is the relative rotation of one end of a shaft with respect to the other when a torque is applied, measured in radians or other angular units.
Q: Why is the polar moment of inertia important?
A: The polar moment of inertia (\( J \)) quantifies the shaft's resistance to torsional deformation, depending on its cross-sectional shape.
Q: How is the angle of twist used in real life?
A: It is used in designing mechanical components like drive shafts, axles, and torsion bars to ensure they can handle applied torques without excessive twisting.
6. Shear Modulus of Typical Engineering Materials
If you don't know the shear modulus of the shaft material, you'll probably find it in the following list:
| Material |
Shear Modulus (\( G \)) |
| Aluminum wrought alloys 2014-T6 |
27 GPa (3.9 × 10⁶ psi) |
| Aluminum wrought alloys 6061-T6 |
26 GPa (3.8 × 10⁶ psi) |
| Cast iron alloys Gray ASTM 20 |
27 GPa (3.9 × 10⁶ psi) |
| Cast iron alloys Malleable ASTM A-197 |
68 GPa (9.9 × 10⁶ psi) |
| Copper alloys Red Brass C83400 |
37 GPa (5.4 × 10⁶ psi) |
| Copper alloys Bronze C86100 |
38 GPa (5.5 × 10⁶ psi) |
| Magnesium alloy Am 1004-T61 |
18 GPa (2.6 × 10⁶ psi) |
| Steel alloys Structural A-36 |
75 GPa (10.9 × 10⁶ psi) |
| Steel alloys Structural A992 |
75 GPa (10.9 × 10⁶ psi) |
| Steel alloys Stainless 304 |
75 GPa (10.9 × 10⁶ psi) |
| Steel alloys Tool L2 |
75 GPa (10.9 × 10⁶ psi) |
| Titanium alloy Ti-6Al-4V |
44 GPa (6.4 × 10⁶ psi) |
Source: Hibbeler RC “Mechanics of Materials in SI units, 10th edition“ Pearson Educación (2017).
Angle of Twist Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back