Angle of Refraction Calculator

Angle of Incidence (\( \theta_1 \)) (degrees):

Refractive Index of Medium 1 (\( n_1 \)):

Refractive Index of Medium 2 (\( n_2 \)):

1. What is the Angle of Refraction Calculator?

Definition: This calculator computes the angle of refraction (\( \theta_2 \)) using Snell's Law, which describes how light bends when passing from one medium to another.

Purpose: It is used in optics, physics, and engineering to analyze light behavior in lenses, prisms, and other optical devices.

2. How Does the Calculator Work?

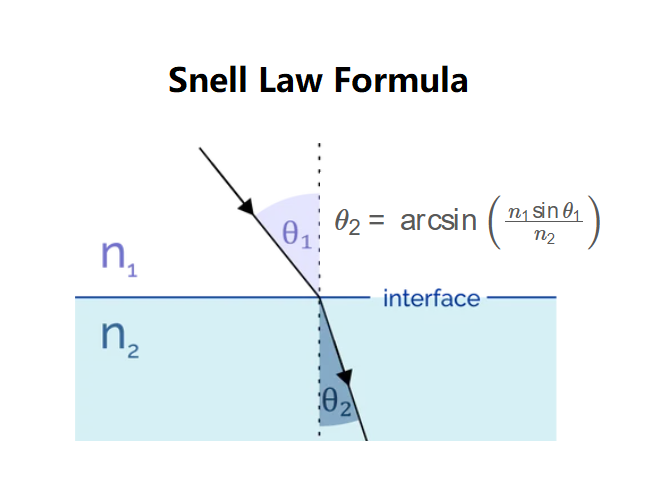
The calculator uses Snell's Law: \( n_1 \sin \theta_1 = n_2 \sin \theta_2 \), rearranged as:

\( \theta_2 = \arcsin\left(\frac{n_1 \sin \theta_1}{n_2}\right) \)

Where:

\( \theta_1 \): Angle of incidence (degrees);
\( n_1 \): Refractive index of medium 1;
\( n_2 \): Refractive index of medium 2;
\( \theta_2 \): Angle of refraction (degrees).

Steps:

Enter the angle of incidence (\( \theta_1 \)) in degrees.
Select or enter the refractive index of medium 1 (\( n_1 \)).
Select or enter the refractive index of medium 2 (\( n_2 \)).
Calculate \( \sin \theta_2 \) using Snell's Law.
Compute \( \theta_2 \) using the arcsine function and convert to degrees.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Angle of Refraction Calculation

Calculating the angle of refraction is crucial for:

Optics Design: Creating lenses, prisms, and optical instruments.
Physics Education: Understanding light behavior.
Engineering Applications: Designing fiber optics and imaging systems.

4. Using the Calculator

Example 1: Calculate the angle of refraction for light traveling from air to water with an incidence angle of 30°:

Angle of Incidence: \( \theta_1 = 30^\circ \);
Refractive Index of Medium 1 (Air): \( n_1 = 1.000273 \);
Refractive Index of Medium 2 (Water): \( n_2 = 1.333 \);
\( \sin \theta_2 = \frac{n_1 \sin \theta_1}{n_2} = \frac{1.000273 \times \sin 30^\circ}{1.333} \approx \frac{1.000273 \times 0.5}{1.333} \approx 0.375 \);
\( \theta_2 = \arcsin(0.375) \approx 22.02^\circ \);
Result: \( \theta_2 = 22.0200^\circ \).

Example 2: Calculate the angle of refraction for light traveling from diamond to vacuum with an incidence angle of 20°:

Angle of Incidence: \( \theta_1 = 20^\circ \);
Refractive Index of Medium 1 (Diamond): \( n_1 = 2.419 \);
Refractive Index of Medium 2 (Vacuum): \( n_2 = 1.0000 \);
\( \sin \theta_2 = \frac{n_1 \sin \theta_1}{n_2} = \frac{2.419 \times \sin 20^\circ}{1.0000} \approx 2.419 \times 0.342 \approx 0.827 \);
\( \theta_2 = \arcsin(0.827) \approx 55.84^\circ \);
Result: \( \theta_2 = 55.8400^\circ \).

5. Frequently Asked Questions (FAQ)

Q: What is Snell's Law?
A: Snell's Law states that \( n_1 \sin \theta_1 = n_2 \sin \theta_2 \), relating the angles of incidence and refraction to the refractive indices of the media.

Q: What happens if \( \sin \theta_2 > 1 \)?
A: This indicates total internal reflection, where light cannot pass into the second medium and is reflected back into the first medium.

Q: Does this calculator account for wavelength-dependent refraction?
A: No, this calculator uses approximate refractive indices and assumes monochromatic light. In reality, refractive indices vary with wavelength (dispersion).