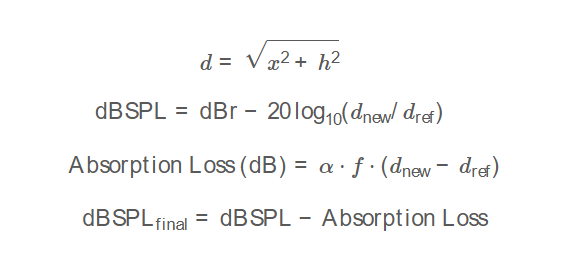Airplane Noise Calculator

Reference Sound Pressure Level (SPL): dB

Reference Horizontal Distance (\( x_{\text{ref}} \)):

Reference Altitude (\( h_{\text{ref}} \)):

New Horizontal Distance (\( x_{\text{new}} \)):

New Altitude (\( h_{\text{new}} \)):

Frequency (for absorption, optional):

Note: This is a simplified estimate based on the inverse square law and basic absorption. Actual airplane noise varies with factors like aircraft type, engine power, humidity, temperature, and terrain. For precise measurements, consult an acoustics expert.

1. What is an Airplane Noise Calculator?

Definition: This calculator estimates the sound pressure level (SPL) of airplane noise at a given position, accounting for the inverse square law, the effect of altitude, and optional frequency-dependent absorption.

Purpose: It helps residents near airports, aviation planners, and engineers estimate noise levels to assess impact or plan mitigation strategies, such as adjusting flight paths.

2. How Does the Calculator Work?

The calculator uses the following method to estimate noise levels:

Formulas: \[ d = \sqrt{x^2 + h^2} \] \[ \text{dBSPL} = \text{dBr} - 20 \log_{10}(d_{\text{new}} / d_{\text{ref}}) \] Optional absorption (if frequency is provided): \[ \text{Absorption Loss (dB)} = \alpha \cdot f \cdot (d_{\text{new}} - d_{\text{ref}}) \] \[ \text{dBSPL}_{\text{final}} = \text{dBSPL} - \text{Absorption Loss} \] Where:

\( d \): Slant distance (m)
\( x \): Horizontal distance (m)
\( h \): Altitude (m)
\( \text{dBSPL} \): Sound pressure level at new position (dB)
\( \text{dBr} \): Reference SPL at reference position (dB)
\( d_{\text{ref}} \): Reference slant distance (m)
\( d_{\text{new}} \): New slant distance (m)
\( \alpha \): Absorption coefficient (0.01 dB/(kHz·m), simplified)
\( f \): Frequency (kHz)

Unit Conversions:

Distance and Altitude:

1 km = 1000 m
1 cm = 0.01 m
1 mi = 1609.344 m
1 ft = 0.3048 m
1 in = 0.0254 m

Frequency:

1 kHz = 1000 Hz

Steps:

Enter the reference SPL (dB) at a known reference position, defined by its horizontal distance and altitude, selecting the units.
Enter the new position’s horizontal distance and altitude, selecting the units.
Convert all distances and altitudes to meters and compute the slant distances \( d_{\text{ref}} \) and \( d_{\text{new}} \).
Optionally, enter the frequency to include absorption effects (set to 0 to ignore), selecting the unit (Hz or kHz).
Compute the SPL using the inverse square law formula.
If frequency is provided, subtract the absorption loss.
Display the result in dB, rounded to 2 decimal places.

3. Importance of Airplane Noise Calculations

Estimating airplane noise is crucial for:

Community Impact: Assessing noise pollution for residents near airports.
Health: Reducing exposure to high noise levels, which can cause hearing loss, stress, and fatigue.
Planning: Designing flight paths to minimize noise impact, as suggested by adjusting glide paths.

4. Using the Calculator

Examples:

Example 1 (Using Feet, No Absorption): Reference SPL = 80 dB at \( x_{\text{ref}} = 98.43 \, \text{ft} \) (30 m), \( h_{\text{ref}} = 0 \, \text{ft} \), New Position: \( x_{\text{new}} = 196.85 \, \text{ft} \) (60 m), \( h_{\text{new}} = 0 \, \text{ft} \), Frequency = 0 Hz:
- Convert: \( 98.43 \times 0.3048 = 30 \, \text{m} \), \( 196.85 \times 0.3048 = 60 \, \text{m} \)
- Reference Slant Distance: \( d_{\text{ref}} = \sqrt{30^2 + 0^2} = 30 \, \text{m} \)
- New Slant Distance: \( d_{\text{new}} = \sqrt{60^2 + 0^2} = 60 \, \text{m} \)
- \( \text{dBSPL} = 80 - 20 \log_{10}(60 / 30) \)
- \( \log_{10}(2) \approx 0.3010 \), so \( 20 \times 0.3010 = 6.02 \)
- \( \text{dBSPL} = 80 - 6.02 = 73.98 \, \text{dB} \)
Example 2 (Using Miles and Feet, With Absorption): Reference SPL = 114 dB at \( x_{\text{ref}} = 0.06214 \, \text{mi} \) (100 m), \( h_{\text{ref}} = 328.08 \, \text{ft} \) (100 m), New Position: \( x_{\text{new}} = 0.81214 \, \text{mi} \) (1307 m), \( h_{\text{new}} = 1427.17 \, \text{ft} \) (435 m), Frequency = 1 kHz:
- Convert: \( 0.06214 \times 1609.344 = 100 \, \text{m} \), \( 328.08 \times 0.3048 = 100 \, \text{m} \)
- \( 0.81214 \times 1609.344 = 1307 \, \text{m} \), \( 1427.17 \times 0.3048 = 435 \, \text{m} \)
- Frequency: 1 kHz = 1000 Hz
- Reference Slant Distance: \( d_{\text{ref}} = \sqrt{100^2 + 100^2} = \sqrt{20000} \approx 141.42 \, \text{m} \)
- New Slant Distance: \( d_{\text{new}} = \sqrt{1307^2 + 435^2} = \sqrt{1897894} \approx 1377.64 \, \text{m} \)
- \( \text{dBSPL} = 114 - 20 \log_{10}(1377.64 / 141.42) \)
- \( 1377.64 / 141.42 \approx 9.74 \), \( \log_{10}(9.74) \approx 0.9886 \), so \( 20 \times 0.9886 = 19.77 \)
- \( \text{dBSPL} = 114 - 19.77 = 94.23 \, \text{dB} \)
- Absorption: \( \alpha = 0.01 \), \( f = 1 \, \text{kHz} \), Distance = \( 1377.64 - 141.42 = 1236.22 \, \text{m} \)
- \( \text{Absorption Loss} = 0.01 \times 1 \times 1236.22 = 12.36 \, \text{dB} \)
- \( \text{dBSPL}_{\text{final}} = 94.23 - 12.36 = 81.87 \, \text{dB} \)

5. Frequently Asked Questions (FAQ)

Q: What is a typical SPL for an airplane?
A: Jet aircraft noise can be around 114 dB at a close distance, which is near the threshold of pain. This calculator helps estimate how it decreases with distance and altitude.

Q: Why include altitude in the calculation?
A: Altitude affects the slant distance between the airplane and observer, which is the true path sound travels. Increasing altitude reduces noise, as shown in glide path adjustments.

Q: Why include absorption?
A: Absorption accounts for additional noise reduction due to air, which depends on frequency, humidity, and temperature. This calculator uses a simplified model; real-world absorption varies.

Q: Can this calculator predict exact noise levels?
A: No, this is an estimate. Actual noise depends on aircraft type, engine power, weather conditions, and terrain. For precise measurements, use professional acoustic equipment.