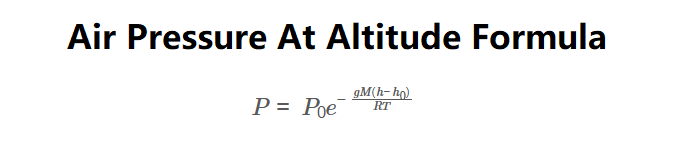Air Pressure at Altitude Calculator

Pressure at Sea Level (\( P_0 \)):

Altitude (\( h \)):

Temperature at Altitude (\( T \)):

Air Pressure (\( P \)):

1. What is the Air Pressure at Altitude Calculator?

Definition: This calculator computes the air pressure (\( P \)) at a given altitude (\( h \)) based on the pressure at sea level (\( P_0 \)) and the temperature at that altitude (\( T \)). Air pressure decreases with increasing altitude due to the reduction in atmospheric mass above.

Purpose: It is used in aviation, meteorology, and engineering to determine air pressure at various altitudes for applications like aircraft performance, weather forecasting, and high-altitude equipment design.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula: \[ P = P_0 e^{-\frac{g M (h - h_0)}{R T}} \] where:

\( P \): Air pressure at altitude \( h \) (Pa, bar, psi, at, atm, Torr, hPa, kPa, lb/ft², mmHg, inHg)
\( P_0 \): Pressure at sea level (Pa, bar, psi, at, atm, Torr, hPa, kPa, lb/ft², mmHg, inHg)
\( h \): Altitude (m, km, ft, mi)
\( h_0 \): Reference altitude, 0 m (sea level)
\( T \): Temperature at altitude \( h \) (K, °C, °F)
\( g \): Acceleration due to gravity, 9.80665 m/s²
\( M \): Molar mass of Earth's air, 0.0289644 kg/mol
\( R \): Universal gas constant, 8.31432 N·m/(mol·K)

Unit Conversions:

Altitude (\( h \)):
- 1 m = 1 m
- 1 km = 1000 m
- 1 ft = 0.3048 m
- 1 mi = 1609.34 m
Temperature (\( T \)):
- 1 °C = 273.15 K
- 1 °F = (T - 32) × 5/9 + 273.15 K
- 1 K = 1 K
Pressure (\( P_0 \), \( P \)):
- 1 Pa = 1 Pa
- 1 bar = 100000 Pa
- 1 psi = 6894.76 Pa
- 1 at = 98066.5 Pa
- 1 atm = 101325 Pa
- 1 Torr = 133.322 Pa
- 1 hPa = 100 Pa
- 1 kPa = 1000 Pa
- 1 lb/ft² = 47.8803 Pa
- 1 mmHg = 133.322 Pa
- 1 inHg = 3386.39 Pa

Steps:

Enter the pressure at sea level (\( P_0 \)) in Pa, bar, psi, at, atm, Torr, hPa, kPa, lb/ft², mmHg, or inHg (default is 101325 Pa, step size 0.00001).
Enter the altitude (\( h \)) in m, km, ft, or mi (default is 0 m, step size 0.00001).
Enter the temperature at altitude (\( T \)) in °C, °F, or K (default is 25°C, step size 0.00001).
Convert pressure to Pa, altitude to meters, and temperature to Kelvin (K).
Calculate the air pressure (\( P \)) using the formula, with \( h_0 = 0 \) m.
Convert the result to the selected unit and display it, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.

3. Importance of Air Pressure at Altitude Calculation

Calculating air pressure at altitude is crucial for:

Aviation: Determining aircraft performance, as air pressure affects lift, engine efficiency, and cabin pressurization.
Meteorology: Understanding atmospheric conditions at different altitudes for weather forecasting.
High-Altitude Engineering: Designing equipment and structures for high-altitude environments, such as weather balloons and mountaineering gear.

4. Using the Calculator

Examples:

Example 1: Calculate the air pressure at an altitude of 0 m, pressure at sea level of 101325 Pa, and temperature of 25°C, with air pressure in Pa:
- Enter \( P_0 = 101325 \) Pa.
- Enter \( h = 0 \) m.
- Enter \( T = 25 \) °C, convert to K: \( 25 + 273.15 = 298.15 \, \text{K} \).
- Air pressure: \( P = 101325 \times e^{-\frac{9.80665 \times 0.0289644 \times (0 - 0)}{8.31432 \times 298.15}} = 101325 \times e^0 = 101325 \, \text{Pa} \).
- Result: \( P = 101325.0000 \, \text{Pa} \).
Example 2: Calculate the air pressure at an altitude of 5 km, pressure at sea level of 29.92 inHg, and temperature of -10°C, with air pressure in mmHg:
- Enter \( P_0 = 29.92 \) inHg, convert to Pa: \( 29.92 \times 3386.39 = 101283.99 \, \text{Pa} \).
- Enter \( h = 5 \) km, convert to m: \( 5 \times 1000 = 5000 \, \text{m} \).
- Enter \( T = -10 \) °C, convert to K: \( -10 + 273.15 = 263.15 \, \text{K} \).
- Air pressure: \( P = 101283.99 \times e^{-\frac{9.80665 \times 0.0289644 \times (5000 - 0)}{8.31432 \times 263.15}} = 101283.99 \times e^{-0.6495} \approx 52709.82 \, \text{Pa} \).
- Convert to mmHg: \( 52709.82 \times 0.00750062 = 395.2985 \).
- Result: \( P = 395.2985 \, \text{mmHg} \).

5. Frequently Asked Questions (FAQ)

Q: Why does air pressure decrease with altitude?
A: Air pressure decreases with altitude because there is less atmospheric mass above to exert pressure. The exponential decrease is due to the gravitational force acting on the air column.

Q: How does temperature affect air pressure at altitude?
A: Higher temperatures increase the denominator in the exponent, leading to a slower decrease in pressure with altitude. Lower temperatures result in a faster decrease in pressure.

Q: Why is the reference altitude set at sea level?
A: Sea level (\( h_0 = 0 \)) is a standard reference point for atmospheric pressure measurements, making calculations consistent and comparable across different locations and conditions.