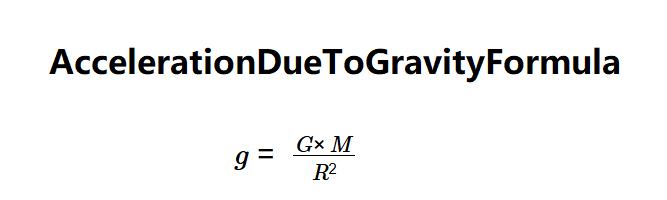Acceleration Due to Gravity Calculator

Mass of Celestial Body (\( M \)):

Radius of Celestial Body (\( R \)):

1. What is the Acceleration Due to Gravity Calculator?

Definition: This calculator computes the acceleration due to gravity (\( g \)) at the surface of a celestial body given its mass (\( M \)) and radius (\( R \)).

Purpose: It is used in physics and astronomy to determine the gravitational acceleration on the surface of planets, moons, or other celestial bodies.

2. How Does the Calculator Work?

The calculator uses the following equation:

\( g = \frac{G \times M}{R^2} \)

Where:

\( M \): Mass of the celestial body (g, kg, t, oz, lb, st, US ton, long ton, Earth masses, Solar masses, \( m_e \), \( m_p \), \( m_n \));
\( R \): Radius of the celestial body (cm, m, km, in, ft, yd, mi, \( R_\oplus \), \( R_\odot \), au, ft/in, m/cm);
\( G \): Universal gravitational constant (\( 6.674 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2} \));
\( g \): Acceleration due to gravity (m/s², cm/s², g, ft/s², km/h²).

Steps:

Enter the mass of the celestial body (\( M \)) with its unit.
Enter the radius of the celestial body (\( R \)) with its unit (use combined fields for ft/in or m/cm if selected).
Convert the inputs to base units (kg for \( M \), m for \( R \)).
Calculate the acceleration due to gravity: \( g = \frac{G \times M}{R^2} \).
Convert the result to the selected output unit and display \( g \), formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Acceleration Due to Gravity Calculation

Calculating the acceleration due to gravity is crucial for:

Astronomy: Understanding the gravitational environment of celestial bodies.
Space Exploration: Planning missions to other planets or moons.
Physics Education: Demonstrating the principles of gravitational attraction.

4. Using the Calculator

Example 1 (Earth): Calculate the acceleration due to gravity on Earth's surface:

Mass: \( M = 5.972 \times 10^{24} \, \text{kg} \);
Radius: \( R = 1 \, \text{Earth radius} = 6,371,000 \, \text{m} \);
Gravity: \( g = \frac{(6.674 \times 10^{-11}) \times (5.972 \times 10^{24})}{(6,371,000)^2} \approx 9.820 \, \text{m/s}^2 \);
Result: \( g = 9.8200 \, \text{m/s}^2 \).

Example 2 (Sun): Calculate the acceleration due to gravity on the Sun's surface:

Mass: \( M = 1 \, \text{Solar mass} = 1.989 \times 10^{30} \, \text{kg} \);
Radius: \( R = 1 \, \text{Solar radius} = 695,700,000 \, \text{m} \);
Gravity: \( g = \frac{(6.674 \times 10^{-11}) \times (1.989 \times 10^{30})}{(695,700,000)^2} \approx 274.1 \, \text{m/s}^2 \);
Result: \( g = 274.1000 \, \text{m/s}^2 \).

5. Frequently Asked Questions (FAQ)

Q: Why is the acceleration due to gravity independent of an object's mass?
A: The formula \( g = \frac{G \times M}{R^2} \) depends only on the mass and radius of the celestial body, not the mass of the object experiencing the gravity.

Q: Why does the Sun have more gravity than Earth?
A: The Sun has a much larger mass (\( 1.989 \times 10^{30} \, \text{kg} \)) compared to Earth (\( 5.972 \times 10^{24} \, \text{kg} \)), resulting in a much higher gravitational acceleration at its surface.

Q: Can this calculator be used for non-spherical bodies?
A: This calculator assumes a spherical, uniform mass distribution. For non-spherical or irregular bodies, the gravitational field may vary and require more complex calculations.