Unit Circle Calculator

1. What is a Unit Circle Calculator?

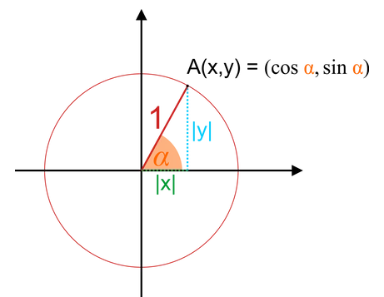
Definition: This calculator computes the x-coordinate, y-coordinate, and tangent of an angle on the unit circle, where the radius is 1.

Purpose: It is used in trigonometry to determine the sine, cosine, and tangent values of an angle, useful in mathematics, physics, and engineering.

2. How Does the Calculator Work?

The calculator uses the following formulas for a unit circle (radius = 1):

X-coordinate \( x \): \( x = \cos(\alpha) \)
Y-coordinate \( y \): \( y = \sin(\alpha) \)
Tangent \( \tan(\alpha) \): \( \tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} \), undefined when \( \cos(\alpha) = 0 \)

Steps:

Input the angle \( \alpha \) in degrees (0 to 360).
Convert the angle to radians for calculation.
Validate the input angle.
Calculate \( x \), \( y \), and \( \tan(\alpha) \), handling undefined tangent cases.
Display the results, formatted to 4 decimal places or in scientific notation for very small values.

3. Importance of Unit Circle Calculations

Calculating unit circle values is crucial for:

Trigonometry Education: Understanding the relationship between angles and trigonometric functions.
Physics: Analyzing periodic phenomena like waves and oscillations.
Engineering: Solving problems involving angles and rotations.

4. Using the Calculator

Examples:

Example 1: For an angle \( \alpha = 30^\circ \):
- X-coordinate \( x \): \( x = \cos(30^\circ) \approx 0.8660 \)
- Y-coordinate \( y \): \( y = \sin(30^\circ) = 0.5000 \)
- Tangent \( \tan(\alpha) \): \( \tan(30^\circ) \approx 0.5774 \)
Example 2: For an angle \( \alpha = 90^\circ \):
- X-coordinate \( x \): \( x = \cos(90^\circ) = 0.0000 \)
- Y-coordinate \( y \): \( y = \sin(90^\circ) = 1.0000 \)
- Tangent \( \tan(\alpha) \): \( \tan(90^\circ) = \text{undefined} \)
Example 3: For an angle \( \alpha = 180^\circ \):
- X-coordinate \( x \): \( x = \cos(180^\circ) = -1.0000 \)
- Y-coordinate \( y \): \( y = \sin(180^\circ) = 0.0000 \)
- Tangent \( \tan(\alpha) \): \( \tan(180^\circ) = 0.0000 \)

5. Frequently Asked Questions (FAQ)

Q: What is the unit circle?
A: The unit circle is a circle with a radius of 1 centered at the origin. It is used to define trigonometric functions, where the x-coordinate is \( \cos(\alpha) \) and the y-coordinate is \( \sin(\alpha) \).

Q: Why is the unit circle important?
A: It provides a geometric interpretation of trigonometric functions and is fundamental in mathematics, physics, and engineering for solving problems involving angles.