Triangular Numbers Calculator

1. What is the Triangular Numbers Calculator?

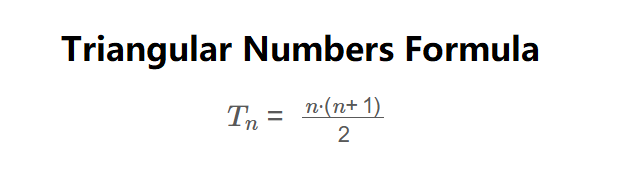
Definition: This calculator computes the \( n \)-th triangular number, which is the sum of the first \( n \) natural numbers, i.e., \( T_n = 1 + 2 + \ldots + n \).

Purpose: It helps users find triangular numbers quickly, useful in mathematics education, number theory, and pattern recognition.

2. How Does the Calculator Work?

The calculator computes the \( n \)-th triangular number using the formula:

\( T_n = \frac{n \cdot (n+1)}{2} \)

Steps:

Enter the position \( n \) (a positive integer).
Click "Calculate" to compute the triangular number.
The result displays the \( n \)-th triangular number.

3. Importance of Triangular Numbers

Triangular numbers are important for:

Mathematics Education: Teaches students about number patterns and sequences.
Number Theory: Appear in various mathematical problems and identities.
Geometry: Represent the number of dots in a triangular arrangement.
Applications: Used in combinatorics, such as calculating combinations or handshakes.

4. Using the Calculator

Example 1 (Small Number): Find the 5th triangular number:

Input: Position (\( n \)): 5;
Result: \( T_5 = \frac{5 \cdot (5+1)}{2} = \frac{5 \cdot 6}{2} = 15 \).

Example 2 (Larger Number): Find the 10th triangular number:

Input: Position (\( n \)): 10;
Result: \( T_{10} = \frac{10 \cdot (10+1)}{2} = \frac{10 \cdot 11}{2} = 55 \).

5. Frequently Asked Questions (FAQ)

Q: What is a triangular number?
A: A triangular number is the sum of the first \( n \) natural numbers, e.g., the 5th triangular number is \( 1 + 2 + 3 + 4 + 5 = 15 \).

Q: Why must the input be a positive integer?
A: Triangular numbers are defined for positive integers, as they represent the sum of natural numbers starting from 1.

Q: What happens if the input is too large?
A: The calculator checks for overflow and displays an error if the position or result exceeds safe limits.