Triangle Area Calculator

Mode:

Base \( b \):

Height \( h \):

Area:

1. What is a Triangle Area Calculator?

Definition: This calculator computes the area of a triangle using different input methods: base and height, three sides, two sides and the angle between them, or two angles and the side between them.

Purpose: It is used in geometry to determine the area of triangles, useful in education, design, and engineering.

2. How Does the Calculator Work?

The calculator operates in four modes:

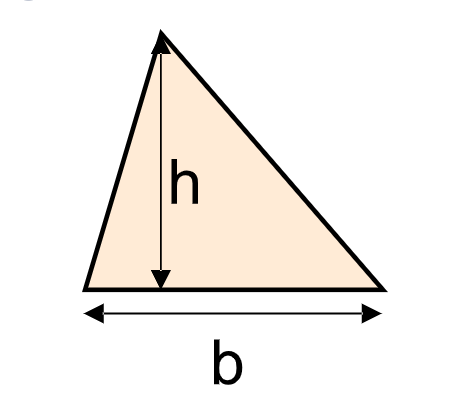
Base and Height Mode:

Area: \( \text{Area} = 0.5 \times b \times h \)

Three Sides (SSS) Mode (Heron's Formula):

Area: \( \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \), where \( s = \frac{a + b + c}{2} \)

Two Sides and Angle Between (SAS) Mode:

Area: \( \text{Area} = 0.5 \times a \times b \times \sin(\gamma) \)

Two Angles and Side Between (ASA) Mode:

Area: \( \text{Area} = \frac{a^2 \times \sin(\beta) \times \sin(\gamma)}{2 \times \sin(\beta + \gamma)} \)

Unit Conversions:

Input Dimensions: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd)
Output Area: m², cm² (1 m² = 10000 cm²), mm² (1 m² = 1000000 mm²), in² (1 m² = 1550.0031 in²), ft² (1 m² = 10.7639 ft²), yd² (1 m² = 1.19599 yd²)

Steps:

Select the mode (Base and Height, Three Sides, Two Sides + Angle Between, or Two Angles + Side Between).
View the corresponding triangle diagram for the selected mode.
Input the required values with their units.
Convert all dimensions to meters for calculation.
Validate the inputs (e.g., triangle inequality, angle constraints).
Calculate the area based on the mode's formula, formatted to 4 decimal places.

3. Importance of Triangle Area Calculations

Calculating the area of a triangle is crucial for:

Geometry Education: Understanding fundamental area formulas and their applications.
Engineering Design: Determining surface areas in triangular components.
Construction: Calculating material needs for triangular shapes.

4. Using the Calculator

Examples:

Example 1 (Base and Height Mode): For a triangle with \( b = 4 \, \text{cm} \), \( h = 3 \, \text{cm} \):
- Convert: \( b = 0.04 \, \text{m} \), \( h = 0.03 \, \text{m} \)
- Area: \( \text{Area} = 0.5 \times 0.04 \times 0.03 = 0.0006 \, \text{m}^2 \)
- Convert: \( \text{Area} = 6 \, \text{cm}^2 \)
Example 2 (Three Sides Mode): For a triangle with \( a = 3 \, \text{cm} \), \( b = 4 \, \text{cm} \), \( c = 5 \, \text{cm} \):
- Convert: \( a = 0.03 \, \text{m} \), \( b = 0.04 \, \text{m} \), \( c = 0.05 \, \text{m} \)
- Semi-perimeter \( s \): \( s = \frac{0.03 + 0.04 + 0.05}{2} = 0.06 \, \text{m} \)
- Area: \( \text{Area} = \sqrt{0.06 \times (0.06 - 0.03) \times (0.06 - 0.04) \times (0.06 - 0.05)} \approx 0.0006 \, \text{m}^2 \)
- Convert: \( \text{Area} = 6 \, \text{cm}^2 \)
Example 3 (Two Sides + Angle Between Mode): For a triangle with \( a = 5 \, \text{cm} \), \( \gamma = 30^\circ \), \( b = 6 \, \text{cm} \):
- Convert: \( a = 0.05 \, \text{m} \), \( b = 0.06 \, \text{m} \)
- Area: \( \text{Area} = 0.5 \times 0.05 \times 0.06 \times \sin(30^\circ) = 0.00075 \, \text{m}^2 \)
- Convert: \( \text{Area} = 7.5 \, \text{cm}^2 \)
Example 4 (Two Angles + Side Between Mode): For a triangle with \( \beta = 60^\circ \), \( a = 4 \, \text{cm} \), \( \gamma = 70^\circ \):
- Convert: \( a = 0.04 \, \text{m} \)
- Area: \( \text{Area} = \frac{0.04^2 \times \sin(60^\circ) \times \sin(70^\circ)}{2 \times \sin(60^\circ + 70^\circ)} \approx 0.000651 \, \text{m}^2 \)
- Convert: \( \text{Area} \approx 6.51 \, \text{cm}^2 \)

5. Frequently Asked Questions (FAQ)

Q: How do you find the area of a triangle?
A: Depending on the given data, you can use the base-height formula, Heron's formula, trigonometry with two sides and the angle between, or the law of sines with two angles and a side.

Q: Why is calculating triangle area important?
A: It is essential for solving problems in geometry, engineering, and construction involving triangular shapes.