Triangle Angle Calculator

Triangle Angle Calculator - Calculating Triangle Sides and Angles

Mode:

Side Length \( a \):

Side Length \( b \):

Side Length \( c \):

Angle \( \alpha \) (degrees):

Angle \( \beta \) (degrees):

Angle \( \gamma \) (degrees):

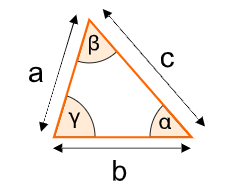
1. What is a Triangle Angle Calculator?

Definition: This calculator computes the angles of a triangle using different input methods: three sides, an angle and two sides, or two angles.

Purpose: It is used in geometry to determine triangle angles, useful in education, design, and engineering.

2. How Does the Calculator Work?

The calculator operates in three modes:

Three Sides (SSS) Mode:

Angle \( \alpha \): \( \alpha = \arccos\left(\frac{b^2 + c^2 - a^2}{2bc}\right) \)
Angle \( \beta \): \( \beta = \arccos\left(\frac{a^2 + c^2 - b^2}{2ac}\right) \)
Angle \( \gamma \): \( \gamma = \arccos\left(\frac{a^2 + b^2 - c^2}{2ab}\right) \)

Angle and Two Sides (SAS) Mode:

If given \( \alpha \), \( a \), \( b \):
- Side \( c \): \( c = \sqrt{a^2 + b^2 - 2ab \cos(\alpha)} \)
- Angle \( \beta \): \( \beta = \arcsin\left(\frac{b \sin(\alpha)}{c}\right) \)
- Angle \( \gamma \): \( \gamma = 180^\circ - \alpha - \beta \)
If given \( \beta \), \( a \), \( b \):
- Side \( c \): \( c = \sqrt{a^2 + b^2 - 2ab \cos(\beta)} \)
- Angle \( \alpha \): \( \alpha = \arcsin\left(\frac{a \sin(\beta)}{c}\right) \)
- Angle \( \gamma \): \( \gamma = 180^\circ - \alpha - \beta \)
If given \( \gamma \), \( a \), \( b \):
- Side \( c \): \( c = \sqrt{a^2 + b^2 - 2ab \cos(\gamma)} \)
- Angle \( \alpha \): \( \alpha = \arccos\left(\frac{b^2 + c^2 - a^2}{2bc}\right) \)
- Angle \( \beta \): \( \beta = 180^\circ - \alpha - \gamma \)

Two Angles (AA) Mode:

Angle \( \gamma \): \( \gamma = 180^\circ - \alpha - \beta \)

Unit Conversions:

Input Dimensions: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd)
Output Dimensions: m, cm, mm, in, ft, yd

Steps:

Select the mode (Three Sides, Angle and Two Sides, or Two Angles).
View the corresponding triangle diagram for the selected mode.
For Angle and Two Sides mode, choose the known angle (\( \alpha \), \( \beta \), or \( \gamma \)).
Input the required values with their units.
Convert all dimensions to meters for calculation.
Validate the inputs (e.g., triangle inequality, angle constraints).
Calculate the outputs based on the mode's formulas, formatted to 4 decimal places.

3. Importance of Triangle Angle Calculations

Calculating triangle angles is crucial for:

Geometry Education: Understanding trigonometric laws and triangle properties.
Engineering Design: Analyzing angular relationships in structures.
Construction: Ensuring accurate angular measurements for layouts.

4. Using the Calculator

Examples:

Example 1 (Three Sides Mode): For a triangle with \( a = 3 \, \text{cm} \), \( b = 4 \, \text{cm} \), \( c = 5 \, \text{cm} \):
- Convert: \( a = 0.03 \, \text{m} \), \( b = 0.04 \, \text{m} \), \( c = 0.05 \, \text{m} \)
- Angle \( \alpha \): \( \alpha = \arccos\left(\frac{0.04^2 + 0.05^2 - 0.03^2}{2 \times 0.04 \times 0.05}\right) \approx 36.8699^\circ \)
- Angle \( \beta \): \( \beta = \arccos\left(\frac{0.03^2 + 0.05^2 - 0.04^2}{2 \times 0.03 \times 0.05}\right) \approx 53.1301^\circ \)
- Angle \( \gamma \): \( \gamma = \arccos\left(\frac{0.03^2 + 0.04^2 - 0.05^2}{2 \times 0.03 \times 0.04}\right) = 90^\circ \)
Example 2 (Angle and Two Sides Mode, Angle \( \alpha \)): For a triangle with \( \alpha = 30^\circ \), \( a = 5 \, \text{cm} \), \( b = 6 \, \text{cm} \):
- Convert: \( a = 0.05 \, \text{m} \), \( b = 0.06 \, \text{m} \)
- Side \( c \): \( c = \sqrt{0.05^2 + 0.06^2 - 2 \times 0.05 \times 0.06 \times \cos(30^\circ)} \approx 0.0312 \, \text{m} \)
- Angle \( \beta \): \( \beta = \arcsin\left(\frac{0.06 \times \sin(30^\circ)}{0.0312}\right) \approx 66.9725^\circ \)
- Angle \( \gamma \): \( \gamma = 180 - 30 - 66.9725 \approx 83.0275^\circ \)
- Convert: \( c \approx 3.12 \, \text{cm} \)
Example 3 (Two Angles Mode): For a triangle with \( \alpha = 50^\circ \), \( \beta = 60^\circ \):
- Angle \( \gamma \): \( \gamma = 180 - 50 - 60 = 70^\circ \)

5. Frequently Asked Questions (FAQ)

Q: How do you find the angles of a triangle?
A: Depending on the given data, you can use the law of cosines (for three sides), a combination of the law of cosines and law of sines (for an angle and two sides), or the triangle angle sum theorem (for two angles).

Q: Why is calculating triangle angles important?
A: It is essential for solving problems in geometry, engineering, and physics involving triangular shapes.