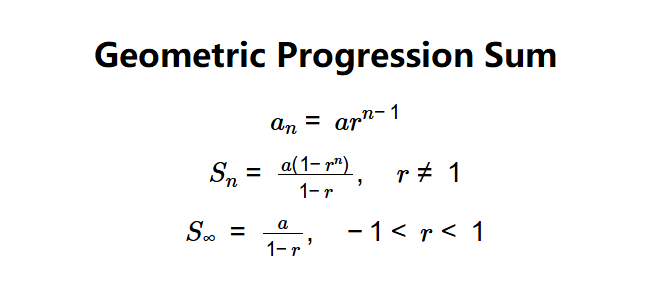Sum of Geometric Progression Calculator

1. What is the Sum of Geometric Progression Calculator?

Definition: This calculator computes the n-th term, the sum of a finite geometric progression, and the sum of an infinite converging geometric series, based on the first term and common ratio of the sequence.

Purpose: Helps students, mathematicians, and financial analysts calculate the total value of a geometric sequence, useful in mathematics, finance (e.g., annuities), and series analysis.

2. How Does the Calculator Work?

The calculator follows a process to compute the required values:

Geometric Progression Formulas:

\( a_n = a r^{n-1} \)

\( S_n = \frac{a (1 - r^n)}{1 - r}, \quad r \neq 1 \)

\( S_\infty = \frac{a}{1 - r}, \quad -1 < r < 1 \)

Where:

\( a \): First term (the scale factor)
\( r \): Common ratio
\( n \): Number of terms

Steps:

Step 1: Obtain the first term and common ratio. Input the initial value (\( a \)) and the factor by which each term increases or decreases (\( r \)).
Step 2: Specify the number of terms. Enter the number of terms (\( n \)) for the finite sum calculation.
Step 3: Calculate the n-th term. Use \( a r^{n-1} \) to find the value of the n-th term.
Step 4: Calculate the sum of n terms. Use \( \frac{a (1 - r^n)}{1 - r} \) if \( r \neq 1 \).
Step 5: Calculate the sum of the infinite series. Use \( \frac{a}{1 - r} \) if the absolute value of the common ratio is less than 1 (\( -1 < r < 1 \)).

3. Importance of Geometric Progression Sums

Calculating these sums is crucial for:

Mathematical Analysis: Provides insights into the behavior of geometric sequences, useful in algebra and calculus.
Financial Applications: Helps in valuing perpetuities, annuities, or compound interest scenarios in finance.
Convergence Study: Determines whether an infinite series converges, essential for theoretical and practical applications.

4. Using the Calculator

Example: First Term = 2, Common Ratio = 0.5, Number of Terms = 4:

Step 1: First Term = 2, Common Ratio = 0.5
Step 2: Number of Terms = 4
Step 3: n-th Term: \( 2 \times 0.5^{4-1} = 2 \times 0.5^3 = 2 \times 0.125 = 0.25 \)
Step 4: Sum of n Terms: \( \frac{2 (1 - 0.5^4)}{1 - 0.5} = \frac{2 (1 - 0.0625)}{0.5} = \frac{2 \times 0.9375}{0.5} = 3.75 \)
Step 5: Sum of Infinite Series: \( \frac{2}{1 - 0.5} = \frac{2}{0.5} = 4.00 \) (since \( |0.5| < 1 \))
Result: n-th Term = 0.25, Sum of n Terms = 3.75, Sum of Infinite Series = 4.00

The sum of 4 terms (3.75) approaches the infinite sum (4.00) as \( n \) increases, confirming convergence.

Example 2: First Term = 1, Common Ratio = 2, Number of Terms = 3:

Step 1: First Term = 1, Common Ratio = 2
Step 2: Number of Terms = 3
Step 3: n-th Term: \( 1 \times 2^{3-1} = 1 \times 2^2 = 4 \)
Step 4: Sum of n Terms: \( \frac{1 (1 - 2^3)}{1 - 2} = \frac{1 (1 - 8)}{-1} = \frac{-7}{-1} = 7 \)
Step 5: Sum of Infinite Series: N/A (since \( |2| > 1 \))
Result: n-th Term = 4.00, Sum of n Terms = 7.00, Sum of Infinite Series = N/A

The infinite sum is undefined as the series diverges with \( r = 2 \).

Example 3: First Term = 3, Common Ratio = -0.3, Number of Terms = 5:

Step 1: First Term = 3, Common Ratio = -0.3
Step 2: Number of Terms = 5
Step 3: n-th Term: \( 3 \times (-0.3)^{5-1} = 3 \times (-0.3)^4 = 3 \times 0.0081 = 0.0243 \)
Step 4: Sum of n Terms: \( \frac{3 (1 - (-0.3)^5)}{1 - (-0.3)} = \frac{3 (1 - (-0.00243))}{1.3} = \frac{3 \times 1.00243}{1.3} \approx 2.31 \)
Step 5: Sum of Infinite Series: \( \frac{3}{1 - (-0.3)} = \frac{3}{1.3} \approx 2.31 \) (since \( |-0.3| < 1 \))
Result: n-th Term = 0.02, Sum of n Terms = 2.31, Sum of Infinite Series = 2.31

The sum of 5 terms (2.31) nears the infinite sum (2.31), confirming convergence with an alternating series.

5. Frequently Asked Questions (FAQ)

Q: What happens if the common ratio is 1?
A: The sum formula \( S_n = \frac{a (1 - r^n)}{1 - r} \) becomes undefined when \( r = 1 \), as division by zero occurs. The series sum is simply \( a \times n \) in this case.

Q: Why is the infinite sum only valid for \( -1 < r < 1 \)?
A: If \( |r| \geq 1 \), the series diverges (grows without bound), making the infinite sum undefined. Convergence requires the terms to approach zero.

Q: How is this used in finance?
A: Geometric series sums are used to calculate the present value of perpetuities or annuities, where a fixed payment grows or shrinks at a constant rate over time.