1. What is the Square Calculator?
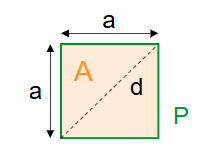
Definition: This calculator computes the area, diagonal, and perimeter of a square based on its side length.
Purpose: It assists in geometry, architecture, and design by providing key measurements of a square, useful in fields like construction, education, and engineering.
2. How Does the Calculator Work?
The calculator uses the following formulas:
- Area (\( A \)): \( A = a^2 \)
- Diagonal (\( d \)): \( d = a \times \sqrt{2} \)
- Perimeter (\( P \)): \( P = 4 \times a \)
Steps:
- Enter the side length (a) with its unit (mm, cm, m, in, ft, or yd).
- Convert the side length to meters for calculation.
- Compute the area, diagonal, and perimeter using the formulas above.
- Convert each result to the user-selected unit (area to mm², cm², m², in², ft², or yd²; diagonal and perimeter to mm, cm, m, in, ft, or yd).
- Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.
3. Importance of Square Calculations
Calculating the properties of a square is essential for:
Construction: Determining material needs for square-shaped areas.
Design: Planning layouts for tiles, rooms, or plots of land.
Education: Teaching geometry concepts related to squares and their properties.
4. Using the Calculator
Example 1: Calculate the properties of a square:
- Side Length: \( a = 4 \, \text{in} \);
- Output Units: Area in square centimeters, Diagonal in centimeters, Perimeter in meters;
- Convert to meters: \( a = 4 \times 0.0254 = 0.1016 \, \text{m} \);
- Area: \( A = (0.1016)^2 \approx 0.01032 \, \text{m}^2 \), in cm²: \( 0.01032 \times 10000 \approx 103.2256 \, \text{cm}^2 \);
- Diagonal: \( d = 0.1016 \times \sqrt{2} \approx 0.1437 \, \text{m} \), in cm: \( 0.1437 \times 100 \approx 14.37 \, \text{cm} \);
- Perimeter: \( P = 4 \times 0.1016 = 0.4064 \, \text{m} \), in meters: \( 0.4064 \, \text{m} \);
- Results:
- Area: \( 103.2256 \, \text{cm}^2 \)
- Diagonal: \( 14.3700 \, \text{cm} \)
- Perimeter: \( 0.4064 \, \text{m} \)
5. Frequently Asked Questions (FAQ)
Q: What is a square?
A: A square is a four-sided polygon with equal sides and right angles (90 degrees).
Q: Why is the side length restricted to positive values?
A: A square cannot have a negative or zero side length, as it represents a physical dimension that must be greater than zero.
Q: How is the diagonal of a square related to its side length?
A: The diagonal of a square is the side length multiplied by \( \sqrt{2} \), derived from the Pythagorean theorem applied to the right triangle formed by two sides and the diagonal.
 Home
Home
 Back
Back