Spiral Length Calculator

Outer Diameter (D):

Inner Diameter (d):

Thickness (t):

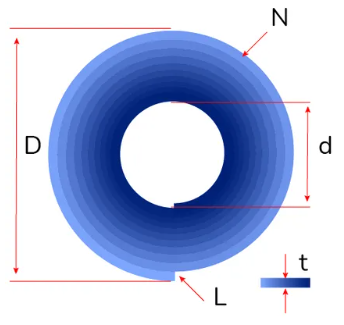
1. What is the Spiral Length Calculator?

Definition: This calculator computes the number of turns and total length of a spiral roll (e.g., a roll of tape) based on the outer diameter, inner diameter, and thickness of the material.

Purpose: It assists in manufacturing, packaging, and engineering by estimating the length of material in a roll, useful for inventory management, design, and production planning.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Number of Turns (\( N \)): \( N = \frac{D - d}{2 \times t} \)
Total Roll Length (\( L \)): \( L = \frac{\pi \times N \times (D + d)}{2} \)

Steps:

Enter the outer diameter (D), inner diameter (d), and thickness (t), each with their respective units (mm, cm, m, in, ft, or yd).
Convert all inputs to meters for calculation.
Compute the number of turns and total roll length using the formulas above.
Convert the total roll length to the user-selected unit (mm, cm, m, in, ft, or yd).
Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Spiral Length Calculations

Calculating the length of a spiral roll is essential for:

Manufacturing:

Packaging:

Education:

4. Using the Calculator

Example 1: Calculate the length of a roll of tape:

Outer Diameter: \( D = 10 \, \text{in} \);
Inner Diameter: \( d = 5 \, \text{cm} \);
Thickness: \( t = 0.1 \, \text{mm} \);
Output Unit for Length: meters;
Convert to meters: \( D = 10 \times 0.0254 = 0.254 \, \text{m} \), \( d = 5 \times 0.01 = 0.05 \, \text{m} \), \( t = 0.1 \times 0.001 = 0.0001 \, \text{m} \);
Number of Turns: \( N = \frac{0.254 - 0.05}{2 \times 0.0001} = 1020 \);
Total Length in m: \( L = \frac{\pi \times 1020 \times (0.254 + 0.05)}{2} \approx 487.26 \, \text{m} \);
Results:
- Number of Turns: \( 1020.0000 \)
- Total Roll Length: \( 487.2600 \, \text{m} \)

5. Frequently Asked Questions (FAQ)

Q: What is a spiral roll?
A: A spiral roll is a material (like tape, paper, or film) wound into a spiral around a central core, with each turn increasing the radius by the thickness of the material.

Q: Why does the inner diameter need to be less than the outer diameter?
A: The inner diameter represents the core of the roll, which must be smaller than the outer diameter of the entire roll for there to be any material wound around it.

Q: What happens if the thickness is too large?
A: If the thickness is too large compared to the difference between the outer and inner diameters, the number of turns becomes invalid (e.g., less than 1), leading to an error in the calculation.