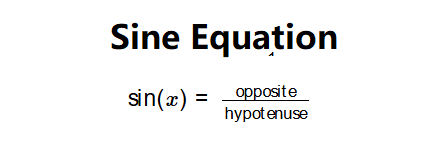1. What is the Sine Calculator?
Definition: This calculator computes the sine (\( \sin(x) \)) of a given angle \( x \). The sine function is one of the fundamental trigonometric functions, defined as the ratio of the opposite side to the hypotenuse in a right triangle, or as the y-coordinate of a point on the unit circle at angle \( x \).
Purpose: The sine function is widely used in mathematics, physics, engineering, and other fields to model periodic phenomena, such as waves, oscillations, and rotations.
2. How Does the Calculator Work?
The calculator computes the sine directly using the \( \sin(x) \) function, where \( x \) must be in radians (PHP's trigonometric functions expect radians as input). In a right triangle, the sine of an angle \( x \) is defined as:
- \( \sin(x) = \frac{\text{opposite}}{\text{hypotenuse}} \)
On the unit circle, \( \sin(x) \) is the y-coordinate of the point at angle \( x \).
Steps:
- Enter the angle \( x \) and select its unit (degrees, radians, etc.).
- Choose the desired precision for the output (number of decimal places).
- The calculator converts the angle to radians and computes \( \sin(x) \).
- The result is displayed with the specified precision.
Unit Conversions (Angles):
- Degrees: \( \text{rad} = \text{deg} \times \frac{\pi}{180} \)
- Radians: No conversion needed
- Gradians: \( \text{rad} = \text{gon} \times \frac{\pi}{200} \)
- Turns: \( \text{rad} = \text{tr} \times 2\pi \)
- Minutes of Arc: \( \text{rad} = \text{deg2rad}(\text{arcmin} / 60) \)
- Seconds of Arc: \( \text{rad} = \text{deg2rad}(\text{arcsec} / 3600) \)
- Milliradians: \( \text{rad} = \text{mrad} / 1000 \)
- Microradians: \( \text{rad} = \text{urad} / 1000000 \)
- π Radians: \( \text{rad} = \text{x π rad} \times \pi \)
3. Properties of the Sine Function
- Domain: The sine function is defined for all real numbers.
- Range: \( \sin(x) \in [-1, 1] \). The sine function takes values between -1 and 1, inclusive.
- Periodicity: The sine function is periodic with a period of \( 2\pi \) radians (or 360 degrees).
- Odd Function: \( \sin(-x) = -\sin(x) \), making it an odd function.
- Key Values:
- \( \sin(0) = 0 \)
- \( \sin\left(\frac{\pi}{2}\right) = 1 \) (or \( 90^\circ \))
- \( \sin(\pi) = 0 \) (or \( 180^\circ \))
- \( \sin\left(\frac{3\pi}{2}\right) = -1 \) (or \( 270^\circ \))
4. Using the Calculator
Example 1:
Calculate \( \sin(30^\circ) \) with 4 decimal places.
- Enter \( x = 30 \), with unit "degrees".
- Select precision as 4 decimal places.
- Click "Calculate" to compute:
- \( \sin(30^\circ) = 0.5 \)
- Displayed as 0.5000 (with 4 decimal places).
Example 2:
Calculate \( \sin\left(\frac{\pi}{3}\right) \) with 3 decimal places.
- Enter \( x = \frac{\pi}{3} \), with unit "radians".
- Select precision as 3 decimal places.
- Click "Calculate" to compute:
- \( \sin\left(\frac{\pi}{3}\right) = \sin(60^\circ) = \frac{\sqrt{3}}{2} \approx 0.866 \)
- Displayed as 0.866 (with 3 decimal places).
5. Frequently Asked Questions (FAQ)
Q: What is the sine function?
A: The sine function, denoted \( \sin(x) \), is a fundamental trigonometric function. In a right triangle, it is the ratio of the opposite side to the hypotenuse. On the unit circle, it is the y-coordinate of the point at angle \( x \).
Q: What is the range of the sine function?
A: The sine function takes values between -1 and 1, inclusive: \( \sin(x) \in [-1, 1] \).
Q: What are the different angle units?
A: Angles can be measured in:
- Degrees: 360° in a full circle.
- Radians: \( 2\pi \) in a full circle.
- Gradians: 400 gon in a full circle.
- Turns: 1 turn is a full circle.
- Minutes of Arc: 60 arcmin per degree.
- Seconds of Arc: 3600 arcsec per degree.
- Milliradians: 1000 mrad per radian.
- Microradians: 1000000 urad per radian.
- π Radians: Expressed as a multiple of π.
 Home
Home
 Back
Back