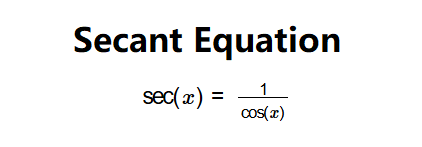1. What is the Secant Calculator?

Definition: This calculator computes the secant (\( \sec(x) \)) of a given angle \( x \). The secant function is the reciprocal of the cosine function, defined as \( \sec(x) = \frac{1}{\cos(x)} \). It is one of the six fundamental trigonometric functions, often used in mathematics, physics, and engineering.

Purpose: The secant function helps describe relationships in right triangles and is useful in various applications, such as wave analysis, navigation, and structural design.

2. How Does the Calculator Work?

The calculator computes the secant using the formula:

In a right triangle, the secant of an angle \( x \) is the ratio of the hypotenuse to the adjacent side:

Steps:

• Enter the angle \( x \) and select its unit (degrees, radians, etc.).
• Choose the desired precision for the output (number of decimal places).
• The calculator converts the angle to radians, computes \( \cos(x) \), and then calculates \( \sec(x) = \frac{1}{\cos(x)} \).
• If \( \cos(x) = 0 \), the secant is undefined, and an error message is displayed.

Unit Conversions (Angles):

• Degrees: \( \text{rad} = \text{deg} \times \frac{\pi}{180} \)
• Radians: No conversion needed
• Gradians: \( \text{rad} = \text{gon} \times \frac{\pi}{200} \)
• Turns: \( \text{rad} = \text{tr} \times 2\pi \)
• Minutes of Arc: \( \text{rad} = \text{deg2rad}(\text{arcmin} / 60) \)
• Seconds of Arc: \( \text{rad} = \text{deg2rad}(\text{arcsec} / 3600) \)
• Milliradians: \( \text{rad} = \text{mrad} / 1000 \)
• Microradians: \( \text{rad} = \text{urad} / 1000000 \)
• π Radians: \( \text{rad} = \text{x π rad} \times \pi \)

3. Properties of the Secant Function

• Domain: The secant function is defined for all angles except where \( \cos(x) = 0 \), i.e., \( x \neq \frac{\pi}{2} + n\pi \), where \( n \) is an integer.
• Range: \( \sec(x) \leq -1 \) or \( \sec(x) \geq 1 \). The secant never takes values between -1 and 1.
• Periodicity: The secant function is periodic with a period of \( 2\pi \) radians (or 360 degrees).
• Even Function: \( \sec(-x) = \sec(x) \), making it an even function.

4. Using the Calculator

Example 1: Calculate \( \sec(45^\circ) \) with 4 decimal places.

1. Enter \( x = 45 \), with unit "degrees".
2. Select precision as 4 decimal places.
3. Click "Calculate" to compute:
   • \( \cos(45^\circ) = \frac{\sqrt{2}}{2} \approx 0.7071 \)
   • \( \sec(45^\circ) = \frac{1}{\cos(45^\circ)} \approx \frac{1}{0.7071} \approx 1.4142 \)

Example 2: Calculate \( \sec(\frac{\pi}{2}) \).

1. Enter \( x = \frac{\pi}{2} \), with unit "radians".
2. Click "Calculate" to compute:
   • \( \cos(\frac{\pi}{2}) = 0 \)
   • \( \sec(\frac{\pi}{2}) = \frac{1}{\cos(\frac{\pi}{2})} \) is undefined (error displayed).

5. Frequently Asked Questions (FAQ)

Q: What is the secant function?
A: The secant function, denoted \( \sec(x) \), is the reciprocal of the cosine function: \( \sec(x) = \frac{1}{\cos(x)} \). In a right triangle, it is the ratio of the hypotenuse to the adjacent side.

Q: When is the secant function undefined?
A: The secant function is undefined when \( \cos(x) = 0 \), which occurs at angles \( x = \frac{\pi}{2} + n\pi \) radians (or \( 90^\circ + n \cdot 180^\circ \)), where \( n \) is an integer.

Q: What are the different angle units?
A: Angles can be measured in:

• Degrees: 360° in a full circle.
• Radians: \( 2\pi \) in a full circle.
• Gradians: 400 gon in a full circle.
• Turns: 1 turn is a full circle.
• Minutes of Arc: 60 arcmin per degree.
• Seconds of Arc: 3600 arcsec per degree.
• Milliradians: 1000 mrad per radian.
• Microradians: 1000000 urad per radian.
• π Radians: Expressed as a multiple of π.

Secant Calculator© - All Rights Reserved 2025