1. What is the Root Calculator?

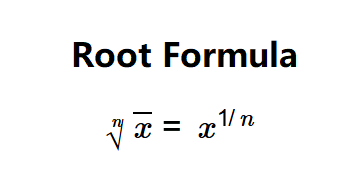
Definition: This calculator computes the nth root of a number, such as square roots (\( n=2 \)), cube roots (\( n=3 \)), and higher-order roots. It handles both positive and negative numbers, returning real roots where possible or indicating if the result is imaginary.

Purpose: It helps users calculate roots of numbers, useful in algebra, geometry, and other mathematical applications, while also handling cases where the result may be imaginary.

2. How Does the Calculator Work?

The calculator computes the nth root using the following approach:

• \( \sqrt[n]{x} = x^{1/n} \)

It handles:

• Positive numbers: Directly computes the nth root.
• Negative numbers:
  • Odd-degree roots: Returns the real root (e.g., \( \sqrt[3]{-8} = -2 \)).
  • Even-degree roots: Indicates the result is imaginary (e.g., \( \sqrt{-4} \)).

Steps:

• Enter the number to find the root of.
• Enter the degree of the root (\( n \), e.g., 2 for square root, 3 for cube root).
• Click "Calculate" to compute the root.
• The result displays the numeric value of the root or indicates if it is imaginary.

3. Importance of Roots

Roots are important for:

• Algebra: Solving equations involving exponents and simplifying expressions.
• Geometry: Calculating dimensions, such as side lengths of squares and cubes.
• Physics and Engineering: Used in formulas involving exponential relationships, like wave equations.
• Education: Helps students understand inverse operations to exponentiation and the behavior of numbers.

4. Using the Calculator

Example 1 (Square Root): Find the square root of 16:

• Input: Number: 16, Root Degree: 2;
• Result: \( \sqrt{16} = 4.0000 \).

Example 2 (Cube Root of Negative Number): Find the cube root of -27:

• Input: Number: -27, Root Degree: 3;
• Result: \( \sqrt[3]{-27} = -3.0000 \).

5. Frequently Asked Questions (FAQ)

Q: Why does the calculator show imaginary results for some inputs?
A: For even-degree roots of negative numbers (e.g., \( \sqrt{-4} \)), the result is not a real number but an imaginary number, as real roots do not exist in these cases.

Q: How does the calculator handle negative numbers?
A: For odd-degree roots, it computes the real root (e.g., \( \sqrt[3]{-8} = -2 \)). For even-degree roots, it indicates the result is imaginary.

Q: Why is the degree restricted to positive integers?
A: The nth root is defined for positive integer degrees in this context to ensure meaningful and standard mathematical results.

Root Calculator© - All Rights Reserved 2025