Regular Polygon Calculator

Perimeter:

Area:

Interior Angle (α):

degrees

Exterior Angle (β):

degrees

Circumcircle Radius (R):

Incircle Radius / Apothem (r):

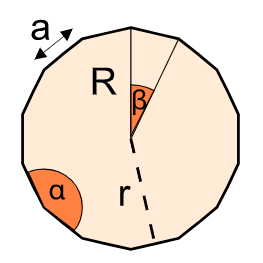
1. What is the Regular Polygon Calculator?

Definition: This calculator computes various properties of a regular polygon, including its perimeter, area, interior and exterior angles, circumcircle radius, and incircle radius (apothem), based on the number of sides and side length.

Purpose: It assists in geometry, design, and engineering by providing key measurements of regular polygons, useful in fields like architecture, graphic design, and education.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Perimeter: \( P = n \times a \)
Area: \( \text{area} = \frac{n \times a^2 \times \cot(\pi/n)}{4} \)
Interior Angle (\( \alpha \)): \( \alpha = \frac{(n - 2) \times \pi}{n} \) (converted to degrees)
Exterior Angle (\( \beta \)): \( \beta = \frac{2 \times \pi}{n} \) (converted to degrees)
Circumcircle Radius (\( R \)): \( R = \frac{a}{2 \times \sin(\pi/n)} \)
Incircle Radius / Apothem (\( r \)): \( r = \frac{a}{2 \times \tan(\pi/n)} \)

Steps:

Enter the number of sides (n) and side length (a) along with its unit (mm, cm, m, in, ft, or yd).
Convert the side length to meters for calculation.
Compute the perimeter, area, angles, circumcircle radius, and incircle radius using the formulas above.
Convert each result to the user-selected unit for that result (lengths to mm, cm, m, in, ft, or yd; area to mm², cm², m², in², ft², or yd²).
Display the angles in degrees.
Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Regular Polygon Calculations

Calculating the properties of regular polygons is essential for:

Architecture:

Graphic Design:

Education:

4. Using the Calculator

Example 1 (Hexagon): Calculate the properties of a regular hexagon:

Number of sides: \( n = 6 \);
Side length: \( a = 4 \, \text{in} \);
Output Units: Perimeter in meters, Area in square inches, Circumradius in inches, Incircle Radius in centimeters;
Convert to meters: \( a = 4 \times 0.0254 = 0.1016 \, \text{m} \);
Perimeter: \( P = 6 \times 0.1016 = 0.6096 \, \text{m} \), in meters: \( 0.6096 \, \text{m} \);
Area: \( \text{area} = \frac{6 \times (0.1016)^2 \times \cot(\pi/6)}{4} \approx 0.02683 \, \text{m}^2 \), in in²: \( 0.02683 \div 0.00064516 \approx 41.5692 \, \text{in}^2 \);
Interior Angle (\( \alpha \)): \( \alpha = \frac{(6 - 2) \times \pi}{6} \), in degrees: \( \alpha = 120 \, \text{degrees} \);
Exterior Angle (\( \beta \)): \( \beta = \frac{2 \times \pi}{6} \), in degrees: \( \beta = 60 \, \text{degrees} \);
Circumcircle Radius (\( R \)): \( R = \frac{0.1016}{2 \times \sin(\pi/6)} \approx 0.1016 \, \text{m} \), in inches: \( 0.1016 \div 0.0254 = 4 \, \text{in} \);
Incircle Radius (\( r \)): \( r = \frac{0.1016}{2 \times \tan(\pi/6)} \approx 0.0879 \, \text{m} \), in centimeters: \( 0.0879 \times 100 \approx 8.79 \, \text{cm} \);
Results:
- Perimeter: \( 0.6096 \, \text{m} \)
- Area: \( 41.5692 \, \text{in}^2 \)
- Interior Angle (\( \alpha \)): \( 120.0000 \, \text{degrees} \)
- Exterior Angle (\( \beta \)): \( 60.0000 \, \text{degrees} \)
- Circumcircle Radius (\( R \)): \( 4.0000 \, \text{in} \)
- Incircle Radius (\( r \)): \( 8.7900 \, \text{cm} \)

5. Frequently Asked Questions (FAQ)

Q: What is a regular polygon?
A: A regular polygon is a polygon with all sides and angles equal. Examples include triangles (n=3), squares (n=4), pentagons (n=5), and hexagons (n=6).

Q: Why is the number of sides restricted to 3 or more?
A: A polygon must have at least 3 sides to form a closed shape. The calculator requires \( n \geq 3 \) to ensure valid geometric calculations.

Q: What is the difference between the circumcircle and incircle radii?
A: The circumcircle radius (\( R \)) is the radius of the circle passing through all vertices of the polygon (circumscribed circle). The incircle radius (\( r \)), or apothem, is the radius of the circle tangent to all sides (inscribed circle), which is also the distance from the center to the midpoint of a side.