1. What is the Radical Calculator?

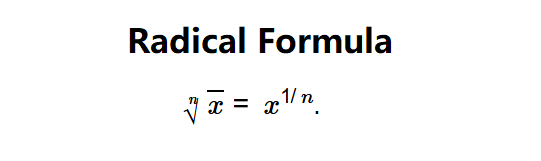
Definition: This calculator computes the nth root (radical) of a positive number, such as square roots (\( n=2 \)), cube roots (\( n=3 \)), or higher-order roots. It provides a simplified form when possible and a numeric approximation.

Purpose: It helps users compute and understand nth roots for both integer and decimal inputs, useful in algebra, geometry, and scientific applications.

2. How Does the Calculator Work?

The calculator computes the nth root using the following steps:

• Computes the numeric value of the nth root: \( \sqrt[n]{x} = x^{1/n} \).
• Checks if the result is a perfect nth root (within a small tolerance).
• If not a perfect root, expresses the result as a radical with the input number.

Steps:

• Enter a positive number (integer or decimal) to find the radical of.
• Enter the degree of the radical (\( n \), e.g., 2 for square root, 3 for cube root, can be decimal).
• Click "Calculate" to compute the radical.
• The result displays the simplified radical form (if perfect) and the numeric value (4 decimal places).

3. Importance of Radicals

Radicals are important for:

• Algebra: Solving equations involving roots and simplifying expressions.
• Geometry: Calculating lengths, areas, and volumes with decimal precision.
• Physics and Engineering: Used in formulas involving exponential relationships, such as fluid dynamics or signal processing.
• Scientific Calculations: Handling non-integer exponents in growth models or statistical analyses.

4. Using the Calculator

Example 1 (Decimal Input): Find the square root of 8.5:

• Input: Number: 8.5, Radical Degree: 2;
• Result: Simplified Radical: \( \sqrt{8.5} \); Numeric Value: \( 2.9155 \).

Example 2 (Fractional Degree): Find the 2.5th root of 16:

• Input: Number: 16, Radical Degree: 2.5;
• Result: Simplified Radical: \( \sqrt[2.5]{16} \); Numeric Value: \( 2.2974 \).

5. Frequently Asked Questions (FAQ)

Q: Why are negative numbers not allowed?
A: Negative numbers can lead to complex results (e.g., imaginary numbers for even-degree roots), so this calculator restricts inputs to positive numbers.

Q: Can I use decimal numbers for the radical degree?
A: Yes, the calculator supports decimal degrees, computing \( x^{1/n} \) for any positive \( n \).

Q: Why is the simplified form sometimes just the radical?
A: If the number is not a perfect nth power, the calculator returns the radical as is, with a numeric approximation.

Radical Calculator© - All Rights Reserved 2025