Powers of i Calculator

1. What is the Powers of i Calculator?

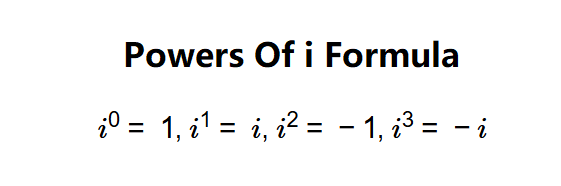
Definition: This calculator computes the result of raising the imaginary unit \( i \) (where \( i = \sqrt{-1} \)) to any integer power \( n \), i.e., \( i^n \). The powers of \( i \) follow a repeating cycle of length 4: \( i^0 = 1 \), \( i^1 = i \), \( i^2 = -1 \), \( i^3 = -i \).

Purpose: It helps users quickly determine the value of \( i^n \) for any integer \( n \), which is useful in complex number arithmetic, algebra, and related fields like physics and engineering.

2. How Does the Calculator Work?

The calculator uses the cyclic property of the powers of \( i \), which repeat every four exponents:

\( i^0 = 1 \), \( i^1 = i \), \( i^2 = -1 \), \( i^3 = -i \)

To compute \( i^n \), the calculator:

Finds the remainder of \( n \) when divided by 4 (i.e., \( n \mod 4 \)).
Adjusts for negative exponents by adding 4 to the remainder if negative.
Maps the remainder to the corresponding value: 0 → 1, 1 → \( i \), 2 → -1, 3 → \( -i \).

Steps:

Enter the exponent \( n \) (an integer).
Click "Calculate" to compute \( i^n \).
The result displays the value of \( i^n \).

3. Importance of Powers of i

The powers of \( i \) are important for:

Complex Numbers: They are fundamental in simplifying expressions involving imaginary and complex numbers.
Algebra: Useful in solving polynomial equations with complex roots.
Physics and Engineering: Appear in oscillatory systems, electrical engineering (e.g., AC circuits), and signal processing.
Mathematics Education: Help students understand the properties of imaginary numbers and cyclic patterns.

4. Using the Calculator

Example 1 (Positive Exponent): Calculate \( i^{123} \):

Input: Exponent: 123;
Result: \( i^{123} = -i \) (since \( 123 \mod 4 = 3 \), and \( i^3 = -i \)).

Example 2 (Negative Exponent): Calculate \( i^{-5} \):

Input: Exponent: -5;
Result: \( i^{-5} = -i \) (since \( -5 \mod 4 = 3 \), and \( i^3 = -i \)).

5. Frequently Asked Questions (FAQ)

Q: What is the imaginary unit \( i \)?
A: The imaginary unit \( i \) is defined as \( i = \sqrt{-1} \), so \( i^2 = -1 \). It is a fundamental concept in complex numbers.

Q: Why do the powers of \( i \) repeat every four exponents?
A: The powers of \( i \) form a cycle because \( i^4 = (i^2)^2 = (-1)^2 = 1 \), and then the pattern repeats: \( i^4 = 1 \), \( i^5 = i \), and so on.

Q: Can this calculator handle negative exponents?
A: Yes, the calculator computes \( i^n \) for any integer \( n \), including negative exponents, by using the cyclic property of \( i \).