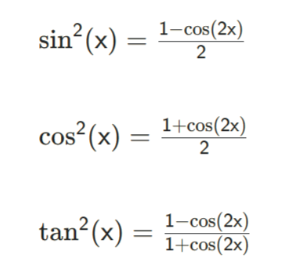Power Reducing Calculator

Mode:

Angle \( \alpha \) (degrees):

\( \sin(x) \):

\( \cos(x) \):

\( \tan(x) \):

\( \sin^2(x) \):

\( \cos^2(x) \):

\( \tan^2(x) \):

1. What is a Power Reducing Calculator?

Definition: This calculator computes trigonometric functions (\(\sin(x)\), \(\cos(x)\), \(\tan(x)\)) and their squared values (\(\sin^2(x)\), \(\cos^2(x)\), \(\tan^2(x)\)) either from an angle or from a given sine or cosine value.

Purpose: It helps in trigonometry to simplify expressions involving squared trigonometric functions, useful in mathematics, physics, and engineering.

2. How Does the Calculator Work?

The calculator operates in two modes:

An Angle Mode:

\( \sin(x) \): \( \sin(x) = \sin(\alpha) \)
\( \cos(x) \): \( \cos(x) = \cos(\alpha) \)
\( \tan(x) \): \( \tan(x) = \frac{\sin(\alpha)}{\cos(\alpha)} \), undefined when \( \cos(\alpha) = 0 \)
\( \sin^2(x) \): \( \sin^2(x) = (\sin(\alpha))^2 \)
\( \cos^2(x) \): \( \cos^2(x) = (\cos(\alpha))^2 \)
\( \tan^2(x) \): \( \tan^2(x) = (\tan(\alpha))^2 \), undefined when \( \cos(\alpha) = 0 \)

One of the Functions Mode:

If given \( \sin(x) \):
- \( \cos(x) \): \( \cos(x) = \sqrt{1 - \sin^2(x)} \) (principal value)
- Angle \( \alpha \): \( \alpha = \arcsin(\sin(x)) \)
If given \( \cos(x) \):
- \( \sin(x) \): \( \sin(x) = \sqrt{1 - \cos^2(x)} \) (principal value)
- Angle \( \alpha \): \( \alpha = \arccos(\cos(x)) \)
\( \tan(x) \): \( \tan(x) = \frac{\sin(x)}{\cos(x)} \), undefined when \( \cos(x) = 0 \)
\( \sin^2(x) \): \( \sin^2(x) = (\sin(x))^2 \)
\( \cos^2(x) \): \( \cos^2(x) = (\cos(x))^2 \)
\( \tan^2(x) \): \( \tan^2(x) = (\tan(x))^2 \), undefined when \( \cos(x) = 0 \)

Steps:

Select the mode (An Angle or One of the Functions).
View the corresponding diagram for the selected mode.
For "One of the Functions" mode, choose the known function (\( \sin(x) \) or \( \cos(x) \)).
Input the required values.
Validate the inputs (e.g., angle between 0 and 360 degrees, \( \sin(x) \) or \( \cos(x) \) between -1 and 1).
Calculate the outputs, formatted to 4 decimal places or in scientific notation for very small values.

3. Importance of Power Reducing Calculations

Power reducing calculations are crucial for:

Trigonometry Education: Simplifying trigonometric identities and expressions.
Physics: Analyzing wave equations and oscillations.
Engineering: Solving problems involving trigonometric functions in design and analysis.

4. Using the Calculator

Examples:

Example 1 (An Angle Mode): For an angle \( \alpha = 30^\circ \):
- \( \sin(x) \): \( \sin(30^\circ) = 0.5000 \)
- \( \cos(x) \): \( \cos(30^\circ) \approx 0.8660 \)
- \( \tan(x) \): \( \tan(30^\circ) \approx 0.5774 \)
- \( \sin^2(x) \): \( (0.5000)^2 = 0.2500 \)
- \( \cos^2(x) \): \( (0.8660)^2 \approx 0.7500 \)
- \( \tan^2(x) \): \( (0.5774)^2 \approx 0.3333 \)
Example 2 (One of the Functions Mode, \( \sin(x) \)): For \( \sin(x) = 0.5 \):
- \( \cos(x) \): \( \cos(x) = \sqrt{1 - (0.5)^2} \approx 0.8660 \)
- \( \tan(x) \): \( \tan(x) = \frac{0.5}{0.8660} \approx 0.5774 \)
- \( \sin^2(x) \): \( (0.5)^2 = 0.2500 \)
- \( \cos^2(x) \): \( (0.8660)^2 \approx 0.7500 \)
- \( \tan^2(x) \): \( (0.5774)^2 \approx 0.3333 \)
- Angle \( \alpha \): \( \alpha = \arcsin(0.5) = 30^\circ \)
Example 3 (One of the Functions Mode, \( \cos(x) \)): For \( \cos(x) = 1 \):
- \( \sin(x) \): \( \sin(x) = \sqrt{1 - (1)^2} = 0.0000 \)
- \( \tan(x) \): \( \tan(x) = \frac{0.0000}{1} = 0.0000 \)
- \( \sin^2(x) \): \( (0.0000)^2 = 0.0000 \)
- \( \cos^2(x) \): \( (1)^2 = 1.0000 \)
- \( \tan^2(x) \): \( (0.0000)^2 = 0.0000 \)
- Angle \( \alpha \): \( \alpha = \arccos(1) = 0^\circ \)

5. Frequently Asked Questions (FAQ)

Q: What are power reducing formulas?
A: Power reducing formulas simplify squared trigonometric functions, such as \( \sin^2(x) \), \( \cos^2(x) \), and \( \tan^2(x) \), often derived from double-angle identities.

Q: Why are power reducing calculations important?
A: They are essential for simplifying trigonometric expressions in mathematics, physics, and engineering applications.