1. What is the Pi Calculator?

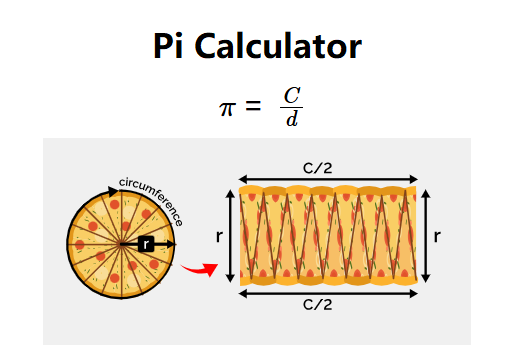
Definition: This calculator estimates the mathematical constant π (pi), which is the ratio of a circle's circumference to its diameter, approximately 3.14159. It uses the direct measurement method by dividing the circumference by the diameter.

Purpose: It allows users to experimentally estimate π by measuring a circular object's circumference and diameter in inches (in) or centimeters (cm), compare it with the actual value, and learn about historical estimates like Archimedes' Theorem.

2. How Does the Calculator Work?

The calculator estimates π using the fundamental geometric relationship:

• \( \pi = \frac{C}{d} \)

where \( C \) is the circumference and \( d \) is the diameter of a circular object, both measured in the same unit (inches or centimeters).

Steps:

• Enter the circumference (\( C \)) and diameter (\( d \)) of a circular object, selecting the unit (in or cm).
• Ensure both measurements use the same unit.
• Click "Calculate" to estimate π and view comparisons.
• The result displays the estimated π, the actual π (15 decimal places), Archimedes' estimate, the percentage difference, and a historical note.

3. Importance of Pi

Pi (π) is crucial for:

• Geometry: Calculating circumferences, areas, and volumes of circular objects.
• Physics: Used in equations involving waves, oscillations, and circular motion.
• Engineering: Essential for designing circular structures like wheels and gears.
• Historical Significance: Ancient civilizations, like the Babylonians, estimated π thousands of years ago, showing its enduring importance.

4. Using the Calculator

Example 1 (Circular Object in Inches): Estimate π with a circumference of 62.8 inches and a diameter of 20 inches:

• Input: Circumference: 62.8 in, Diameter: 20 in;
• Result: Pi (π): 3.1400;
• Actual π (15 decimal places): 3.141592653589793;
• Archimedes' Theorem: 2.0833333333333335;
• Percentage Difference: 0% (approximately).

Example 2 (Circular Object in Centimeters): Estimate π with a circumference of 78.5 cm and a diameter of 25 cm:

• Input: Circumference: 78.5 cm, Diameter: 25 cm;
• Result: Pi (π): 3.1400;
• Actual π (15 decimal places): 3.141592653589793;
• Archimedes' Theorem: 2.0833333333333335;
• Percentage Difference: 0% (approximately).

5. Frequently Asked Questions (FAQ)

Q: Why must circumference and diameter use the same unit (in or cm)?
A: The ratio \( \pi = \frac{C}{d} \) is unitless, so both measurements must be in the same unit (inches or centimeters) to ensure the calculation is correct.

Q: Why is the percentage difference sometimes large?
A: The estimate depends on the accuracy of the measurements. Small errors in measuring circumference or diameter can lead to significant deviations from the actual value of π.

Q: What is the significance of the Archimedes' estimate in the result?
A: Archimedes approximated π as between \( 3\frac{10}{71} \) and \( 3\frac{1}{7} \), with \( \frac{25}{12} \) (approximately 2.0833) being a simplified historical estimate for comparison.

Pi Calculator© - All Rights Reserved 2025