1. What is the Perfect Cube Calculator?

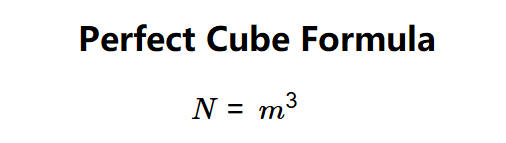
Definition: This calculator determines if a given number is a perfect cube, which is a number that can be expressed as the product of an integer multiplied by itself three times (e.g., \( n \times n \times n \)). If the number is a perfect cube, the calculator also provides its cube root.

Purpose: It helps users quickly identify whether a number is a perfect cube and find its cube root, which is useful in mathematics, number theory, and educational contexts.

2. How Does the Calculator Work?

A number \( N \) is a perfect cube if there exists an integer \( m \) such that:

• \( N = m^3 \)

The calculator computes the cube root of the absolute value of the input number and checks if it is an integer. If so, the number is a perfect cube, and the cube root is returned .

Steps:

• Enter a number (can be positive or negative).
• Click "Calculate" to determine if the number is a perfect cube.
• The result is displayed, indicating whether the number is a perfect cube, and if so, its cube root.

3. Importance of Perfect Cubes

Perfect cubes are important for:

• Mathematics: Understanding number properties and factorization.
• Education: Teaching concepts of exponents and roots, enhancing number sense.
• Applications: Used in geometry for volume calculations (e.g., volume of a cube) and in algebra for solving cubic equations.
• Number Theory: Identifying patterns and properties of numbers.

4. Using the Calculator

Example 1 (Positive Number): Check if 125 is a perfect cube:

• Input: Number: 125;
• Result: The number 125 is a perfect cube. Cube Root: 5 (since \( 5 \times 5 \times 5 = 125 \))

Example 2 (Negative Number): Check if -216 is a perfect cube:

• Input: Number: -216;
• Result: The number -216 is a perfect cube. Cube Root: -6 (since \( (-6) \times (-6) \times (-6) = -216 \)) .

5. Frequently Asked Questions (FAQ)

Q: Can negative numbers be perfect cubes?
A: Yes, negative numbers can be perfect cubes. For example, \( -8 \) is a perfect cube because \( (-2) \times (-2) \times (-2) = -8 \) .

Q: What is the cube root of zero?
A: The cube root of zero is zero, since \( 0 \times 0 \times 0 = 0 \). Thus, 0 is a perfect cube .

Q: How does the calculator determine if a number is a perfect cube?
A: It computes the cube root of the number and checks if it is an integer. If so, the number is a perfect cube, and the integer cube root is displayed

Perfect Cube Calculator© - All Rights Reserved 2025